题目内容
已知正数x、y满足等式x+y-2xy+4=0，则（ ）A．xy的最大值是4，且x+y的最小值是4
B．xy的最小值是4，且x+y的最大值是4
C．xy的最大值是4，且x+y的最大值是4
D．xy的最小值是4，且x+y的最小值是4
【答案】分析：利用x+y≥2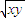
，进行代换、消元，分别得出关于xy，x+y的不等式，通过解不等式考察它们取值范围、确定最值．
解答：解：∵x+y≥2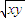
，由已知，0=x+y-2xy+4≥2
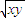-2xy+4．令t=
，-2t2+2t+4≤0，t≥2，（t≤-1舍去）∴xy≥4，当且仅当x=y=2时，取得最小值4．
又xy≤（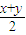
）2，由已知，0=x+y-2xy+4≥x+y-2（
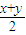）2+4，令μ=x+y，则μ-
μ2+4≤0，μ≥4（μ≤-2舍去），∴x+y≥4，当且仅当x=y=2时，取得最小值4．
故选D．
点评：本题考查基本不等式的应用，考查了转化、换元的思想，不等式解法．
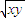，进行代换、消元，分别得出关于xy，x+y的不等式，通过解不等式考察它们取值范围、确定最值．解答：解：∵x+y≥2
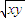，由已知，0=x+y-2xy+4≥2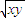-2xy+4．令t=，-2t2+2t+4≤0，t≥2，（t≤-1舍去）∴xy≥4，当且仅当x=y=2时，取得最小值4．又xy≤（
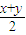）2，由已知，0=x+y-2xy+4≥x+y-2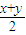（）2+4，令μ=x+y，则μ-μ2+4≤0，μ≥4（μ≤-2舍去），∴x+y≥4，当且仅当x=y=2时，取得最小值4．故选D．
点评：本题考查基本不等式的应用，考查了转化、换元的思想，不等式解法．
练习册系列答案
相关题目