题目内容
(2009•枣庄一模)在平面直角坐标系中,
,
分别是与x,y轴正方向同向的单位向量,平面内三点A、B、C满足
=4
+2
,
=k
-2
,当A、B、C三点构成直角三角形时,实数k的可能值的个数为( )
| i |
| j |
| AB |
| i |
| j |
| AC |
| i |
| j |
分析:由
=4
+2
,
=k
-2
,求出
的坐标,然后分∠A,∠B,∠C为直角利用数量积的坐标表示列式求k得值.
| AB |
| i |
| j |
| AC |
| i |
| j |
| BC |
解答:解:由
=4
+2
,
=k
-2
,
所以
=
-
=(k
-2
)-(4
+2
)=(k-4)
-4
.
若∠A为直角,则
•
=0,即4k-4=0,k=1;
若∠B为直角,则
•
=0,即4(k-4)-8=0,k=6;
若∠C为直角,则
•
=0,即k(k-4)+8=0,次方程无解.
所以实数k的可能值的个数是2个.
故选B.
| AB |
| i |
| j |
| AC |
| i |
| j |
所以
| BC |
| AC |
| AB |
| i |
| j |
| i |
| j |
| i |
| j |
若∠A为直角,则
| AB |
| AC |
若∠B为直角,则
| AB |
| BC |
若∠C为直角,则
| AC |
| BC |
所以实数k的可能值的个数是2个.
故选B.
点评:本题考查了数量积判断两个向量的垂直关系,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目
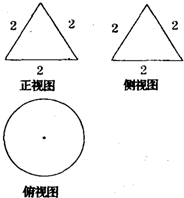 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )