题目内容
20.作边长为1的正三角形的内切圆,在这个圆内做新的内接正三角形,在新的正三角形内再作内切圆,如此继续下去,所有这些圆的面积之和为$\frac{π}{9}$.分析 如图所示,设第n正三角形的内切圆的边角为rn,则r1=$\frac{1}{2}tan\frac{π}{6}$=$\frac{1}{2}×\frac{\sqrt{3}}{3}$,r2=${r}_{1}sin\frac{π}{6}$=$\frac{1}{2}{r}_{1}$,….可得数列$\{{r}_{n}^{2}\}$为等比数列,首项为$(\frac{\sqrt{3}}{6})^{2}$,公比为$\frac{1}{4}$,即可得出.
解答 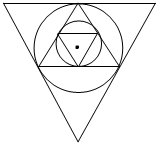 解:如图所示,
解:如图所示,
设第n正三角形的内切圆的边角为rn,
则r1=$\frac{1}{2}tan\frac{π}{6}$=$\frac{1}{2}×\frac{\sqrt{3}}{3}$,r2=${r}_{1}sin\frac{π}{6}$=$\frac{1}{2}{r}_{1}$,….
∴数列$\{{r}_{n}^{2}\}$为等比数列,首项为$(\frac{\sqrt{3}}{6})^{2}$,公比为$\frac{1}{4}$,
∴所有这些圆的面积之和=$\frac{π(\frac{\sqrt{3}}{6})^{2}}{1-\frac{1}{4}}$=$\frac{π}{9}$.
故答案为:$\frac{π}{9}$.
点评 本题考查了正三角形的性质、三角形的内切圆的面积、等比数列的前n项和及其极限,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.已知f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x2,则当x∈(0,+∞)时,f(x)的表达式为( )
| A. | x+x2 | B. | -x+x2 | C. | -x-x2 | D. | x-x2 |
9.如图给出了一个算法流程图,该算法流程图的功能是( )


| A. | 求三个数中最大的数 | B. | 求三个数中最小的数 | ||
| C. | 按从小到大排列 | D. | 按从大到小排列 |
10.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),且$\overrightarrow{a}$•$\overrightarrow{c}$>0,$\overrightarrow{b}$•$\overrightarrow{c}$>0.( )
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$<0,则x>0,y>0 | B. | 若$\overrightarrow{a}$•$\overrightarrow{b}$<0,则x<0,y<0 | ||
| C. | 若$\overrightarrow{a}$•$\overrightarrow{b}$>0,则x<0,y<0 | D. | 若$\overrightarrow{a}$•$\overrightarrow{b}$>0,则x>0,y>0 |