题目内容
已知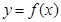 为R上的可导函数,当
为R上的可导函数,当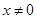 时,
时,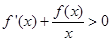 ,则函数
,则函数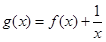 的零点分数为( )
的零点分数为( )
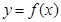 为R上的可导函数,当
为R上的可导函数,当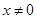 时,
时,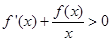 ,则函数
,则函数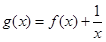 的零点分数为( )
的零点分数为( )| A.1 | B.2 | C.0 | D.0或2 |
C
试题分析:因为函数
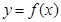 为R上的可导函数,当
为R上的可导函数,当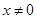 时,
时, 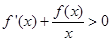 .即可
.即可 .令
.令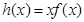 ,即
,即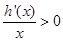 .所以可得
.所以可得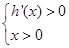 或
或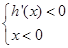 .所以当函数
.所以当函数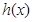 在
在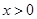 时单调递增,所以
时单调递增,所以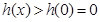 .即函数当
.即函数当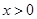 时,
时,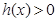 .同理
.同理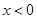 时,
时,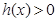 .又因为函数
.又因为函数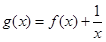 可化为
可化为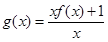 .所以当
.所以当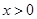 时,
时,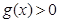 即与x轴没交点.当
即与x轴没交点.当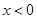 时,
时,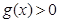 .所以函数
.所以函数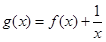 的零点个数为0.故选C.
的零点个数为0.故选C.
练习册系列答案
相关题目
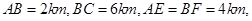 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
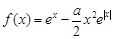 .
.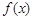 是
是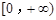 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;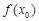 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.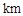 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80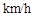 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的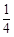 倍,固定成本为a元.
倍,固定成本为a元.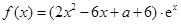 (
(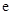 为自然对数的底数).
为自然对数的底数).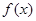 在
在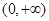 上的单调区间;
上的单调区间;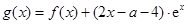 ,是否存在区间
,是否存在区间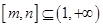 ,使得当
,使得当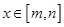 时函数
时函数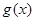 的值域为
的值域为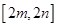 ,若存在求出
,若存在求出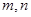 ,若不存在说明理由.
,若不存在说明理由.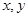 )为函数
)为函数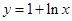 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率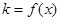 。
。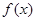 的单调区间;
的单调区间;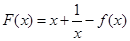 ,求函数
,求函数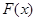 的最小值。
的最小值。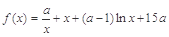 ,
,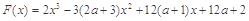 ,其中
,其中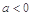 且
且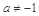 .
. 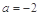 ,求函数
,求函数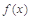 的单调递增区间;
的单调递增区间;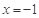 时,函数
时,函数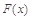 有极值,求函数
有极值,求函数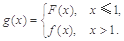 (
(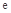 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使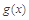 在
在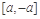 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.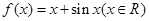 ,且
,且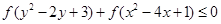 ,则当
,则当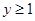 时,
时,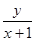 的取值范围是 ( )
的取值范围是 ( )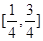
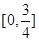
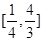
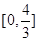
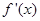 ,且
,且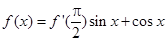 ,则
,则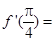 ___.
___.