题目内容
【题目】已知a为实数,函数f(x)=aln x+x2-4x.
(1)是否存在实数a,使得f(x)在x=1处取得极值?证明你的结论;
(2)设g(x)=(a-2)x,若x0∈![]() ,使得f(x0)≤g(x0)成立,求实数a的取值范围.
,使得f(x0)≤g(x0)成立,求实数a的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据反证法求解,利用![]() 求得
求得![]() 后再根据函数的单调性判断,可得结论不成立.(2)问题等价于x0∈
后再根据函数的单调性判断,可得结论不成立.(2)问题等价于x0∈![]() ,使得(x0-ln x0)a≥
,使得(x0-ln x0)a≥![]() -2x0成立,经验证可得x0-ln x0>0,分离参数后得到“x0∈
-2x0成立,经验证可得x0-ln x0>0,分离参数后得到“x0∈![]() ,使得
,使得![]() 成立”,然后令
成立”,然后令![]() ,求出
,求出![]() 的最小值后可得所求的范围.
的最小值后可得所求的范围.
(1)由题意得函数f(x)的定义域为(0,+∞),
∵f(x)=aln x+x2-4x,
∵f′(x)=![]() +2x-4=
+2x-4=![]() .
.
假设存在实数a,使f(x)在x=1处取得极值,
则![]() ,解得a=2,
,解得a=2,
此时,f′(x)=![]() ,
,
当x>0时,f′(x)≥0恒成立,
∴ f(x)在(0,+∞)上单调递增,
∴ x=1不是f(x)的极值点.
故不存在实数a,使得f(x)在x=1处取得极值.
(2)由f(x0)≤g(x0),得(x0-ln x0)a≥x-2x0,
记F(x)=x-ln x(x>0),则F′(x)=![]() (x>0),
(x>0),
∴ 当0<x<1时,F′(x)<0,F(x)单调递减;
当x>1时,F′(x)>0,F(x)单调递增.
∴ F(x)>F(1)=1>0,
∴ a≥![]() ,
,
记G(x)=![]() ,x∈
,x∈![]() ,
,
∴G′(x)=![]() =
=![]() .
.
∵ x∈![]() ,
,
∴ 2-2ln x=2(1-ln x)≥0,
∴ x -2ln x+2>0,
∴ 当x∈![]() 时,G′(x)<0,G(x)单调递减;
时,G′(x)<0,G(x)单调递减;
当x∈(1,e)时,G′(x)>0,G(x)单调递增,
∴ G(x)min=G(1)=-1.
∴ a≥G(x)min=-1.
故实数a的取值范围为[-1,+∞).

【题目】大学的生活丰富多彩,很多学生除了学习本专业的必修课外,还会选择一些选修课来充实自已.甲同学调查了自己班上的![]() 名同学学习选修课的情况,并作出如下表格:
名同学学习选修课的情况,并作出如下表格:
每人选择选修课科数 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)求甲同学班上人均学习选修课科数:
(2)甲同学和乙同学的某门选修课是在同一个班,且该门选修课开始上课的时间是早上![]() ,已知甲同学每次上课都会在
,已知甲同学每次上课都会在![]() 到
到![]() 之间的任意时刻到达教室,乙同学每次上课都会在
之间的任意时刻到达教室,乙同学每次上课都会在![]() 到
到![]() 之间的任意时刻到达教室,求连续
之间的任意时刻到达教室,求连续![]() 天内,甲同学比乙同学早到教室的天数
天内,甲同学比乙同学早到教室的天数![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(1)试估计![]() 岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
(2)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:

(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中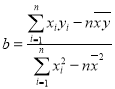 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.