题目内容
若点O是△ABC所在平面内一点,满足3
+
+
=
,则
的值是
| OA |
| OB |
| OC |
| 0 |
| S△ABO |
| S△ABC |
1:5
1:5
.分析:取BC的中点D,则2
=
+
,利用条件可得3
=-2
,进而可求
的值.
| OD |
| OB |
| OC |
| OA |
| OD |
| S△ABO |
| S△ABC |
解答:解:取BC的中点D,则2
=
+
∵3
+
+
=
∴3
=-2
∴
=
∵
=
∴
=1:5
故答案为:1:5
| OD |
| OB |
| OC |
∵3
| OA |
| OB |
| OC |
| 0 |
∴3
| OA |
| OD |
∴
| S△ABO |
| S△ABD |
| 2 |
| 5 |
∵
| S△ABD |
| S△ABC |
| 1 |
| 2 |
∴
| S△ABO |
| S△ABC |
故答案为:1:5
点评:本题考查向量知识的运用,考查三角形面积之比,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
点O是△ABC所在平面上一点,若
+
+2
=
,则△AOC的面积与△ABC的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
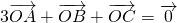 ,则
,则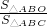 的值是________.
的值是________.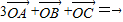 ,则
,则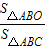 的值是 .
的值是 .