题目内容
已知点O是△ABC所在平面内的一定点,P是平面ABC内一动点,若
=
+λ(
+
),λ∈(0,+∞),则点P的轨迹一定经过△ABC的( )
| OP |
| OA |
| AB |
| 1 |
| 2 |
| BC |
分析:设D是BC的中点,由
+
=
,
=
+λ(
+
),λ∈(0,+∞),知
=
+λ
,所以点P的轨迹是射线AD,故点P的轨迹一定经过△ABC的重心.
| AB |
| 1 |
| 2 |
| BC |
| AD |
| OP |
| OA |
| AB |
| 1 |
| 2 |
| BC |
| OP |
| OA |
| AD |
解答: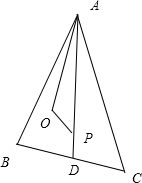 解:如图,设D是BC的中点,
解:如图,设D是BC的中点,
∵
+
=
,
=
+λ(
+
),λ∈(0,+∞),
∴
=
+λ
,
∴点P的轨迹是射线AD,
∵AD是△ABC中BC边上的中线,
∴点P的轨迹一定经过△ABC的重心.
故选B.
 解:如图,设D是BC的中点,
解:如图,设D是BC的中点,∵
| AB |
| 1 |
| 2 |
| BC |
| AD |
| OP |
| OA |
| AB |
| 1 |
| 2 |
| BC |
∴
| OP |
| OA |
| AD |
∴点P的轨迹是射线AD,
∵AD是△ABC中BC边上的中线,
∴点P的轨迹一定经过△ABC的重心.
故选B.
点评:本题考查三角形五心的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,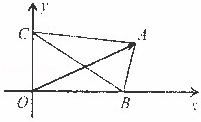
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,| |=|
|=|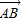 |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,| |=|
|=| |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .
 是三个单位向量,且满足2
是三个单位向量,且满足2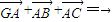 ,|
,| |=|
|=| |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .