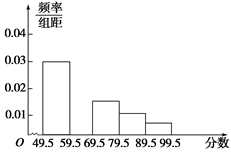
题目内容
关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用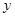 (万元),有如下的统计资料:
(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
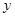 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)(2)估计使用年限为10年时,维修费用是多少?
(1) 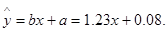 (2) 12.38万元.
(2) 12.38万元.
解析试题分析:(1)根据所给的数据,做出变量x,y的平均数,根据最小二乘法做出线性回归方程的系数b,在根据样本中心点一定在线性回归方程上,求出a的值,从而得到线性回归方程;
(2)当自变量为10时,代入线性回归方程,求出当年的维修费用,这是一个预报值..
试题解析:解:(1)
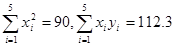
 6分;
6分;
于是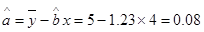 .
.
所以线形回归方程为: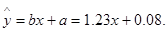 8分;
8分;
(2)当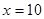 时,
时,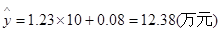 ,
,
即估计使用10年是维修费用是12.38万元. 12分;
考点:线性回归方程..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某工厂有工人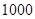 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外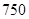 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 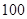 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 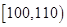 | 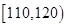 |  | 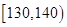 | 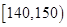 |
| 人数 | 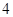 |  |  | 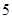 |  |
| 生产能力分组 | 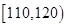 |  | 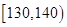 | 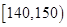 |
| 人数 |  |  |  |  |
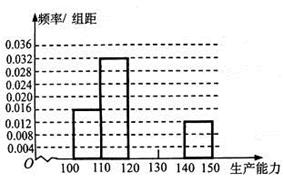
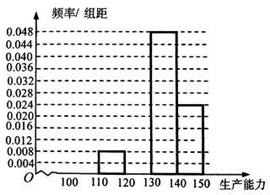
①求
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;②分别估计
 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
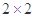 列联表;
列联表;(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
参考公式与临界值表:K2=
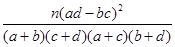
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
| 学历 | 35岁以下 | 35至50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
(2)在该校教师中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取l人,此人的年龄为50岁以上的概率为
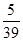 ,求x、y的值.
,求x、y的值. 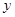 (万元)和房屋的面积
(万元)和房屋的面积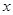 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
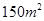 时的销售价格.
时的销售价格.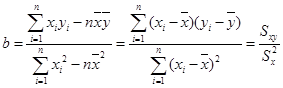
 ,
, ,
,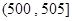 ,
, ,
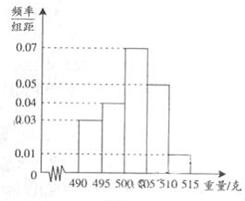
,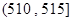 ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题: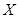 为合格产品的数量,求
为合格产品的数量,求 ;
; 
 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于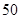 公里和
公里和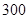 公里之间,将统计结果分
公里之间,将统计结果分 组:
组: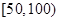 ,
,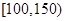 ,
,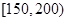 ,
,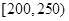 ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
 的值;
的值;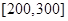 的车辆数;
的车辆数;