题目内容
三棱柱ABC-A1B1C1中,∠BAC=90°,AC⊥BC1,过C1作底面ABC 的垂线C1O,垂足为O,则点O一定落在( )A.直线AB上
B.直线BC上
C.直线CA上
D.△ABC的内部
【答案】分析:由已知中三棱柱ABC-A1B1C1中,∠BAC=90°,AC⊥BC1,由线面垂直的判定定理可得AC⊥平面ABC1,进而再由面面垂直的判定定理得到平面ABC⊥平面ABC1,过C1作底面ABC 的垂线C1O,则垂线C1O应该在平面ABC1上,进而可以得到答案.
解答:解:连接AC1,
∵∠BAC=90°,即AC⊥AB,AC⊥BC1,AB∩BC1=B
∴AC⊥平面ABC1,
∴平面ABC⊥平面ABC1,
若C1O⊥底面ABC
则C1O?平面ABC1,
即O点在直线AB上,
故选A
点评:本题考查的知识点是空间点、线、面的位置关系,其中根据已知条件结合线面垂直和面面垂直的判定定理得到平面ABC⊥平面ABC1,进而得到底面ABC 的垂线C1O,也是BC边上的高是解释本题的关键.
解答:解:连接AC1,
∵∠BAC=90°,即AC⊥AB,AC⊥BC1,AB∩BC1=B
∴AC⊥平面ABC1,
∴平面ABC⊥平面ABC1,
若C1O⊥底面ABC
则C1O?平面ABC1,
即O点在直线AB上,
故选A
点评:本题考查的知识点是空间点、线、面的位置关系,其中根据已知条件结合线面垂直和面面垂直的判定定理得到平面ABC⊥平面ABC1,进而得到底面ABC 的垂线C1O,也是BC边上的高是解释本题的关键.

练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
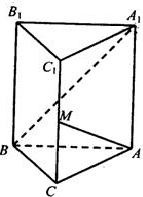 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.