题目内容
如图,设F(-c,0)是椭圆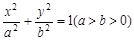 的左焦点,直线l:x=-
的左焦点,直线l:x=-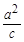 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。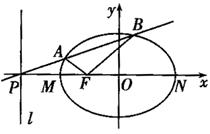
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P的直线m与椭圆相交于不同的两点A,B。
①证明:∠AFM=∠BFN;
②求△ABF面积的最大值。
(Ⅰ)椭圆的标准方程为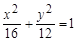 ;(Ⅱ)①详见解析;②
;(Ⅱ)①详见解析;②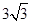 .
.
解析试题分析:(Ⅰ)求椭圆的标准方程,只需利用待定系数法来求,由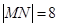 ,知
,知 ,由
,由 ,得
,得 ,将
,将 代入,可求出
代入,可求出 的值,从而得
的值,从而得 的值,由此能求出椭圆的标准方程.(Ⅱ)①证明:
的值,由此能求出椭圆的标准方程.(Ⅱ)①证明: ,只需证明
,只需证明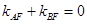 即可,这是直线与二次曲线位置关系问题,可采用设而不求的方法,因此当
即可,这是直线与二次曲线位置关系问题,可采用设而不求的方法,因此当 的斜率为0时,
的斜率为0时, ,满足题意.当
,满足题意.当 的斜率不为0时,可设直线
的斜率不为0时,可设直线 的方程为
的方程为 ,代入椭圆方程得
,代入椭圆方程得 ,设出
,设出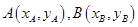 ,有根与系数关系,及斜率公式可得
,有根与系数关系,及斜率公式可得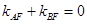 ,从而得到
,从而得到 .故恒有
.故恒有 ;②求△ABF面积的最大值,由图可知
;②求△ABF面积的最大值,由图可知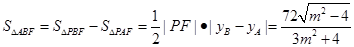 ,由基本不等式,能求出三角形ABF面积的最大值.
,由基本不等式,能求出三角形ABF面积的最大值.
试题解析:(Ⅰ)∵|MN|=8, ∴a=4, (1分)
又∵|PM|=2|MF|,∴e= , (2分)
, (2分)
∴c=2,b2=a2-c2=12,
∴椭圆的标准方程为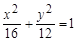 (3分)
(3分)
(Ⅱ)①证明:
当AB的斜率为0时,显然∠AFM=∠BFN=0,满足题意; (4分)
当AB的斜率不为0时,设AB的方程为x=my-8,
代入椭圆方程整理得(3m2+4)y2-48my+144=0. (5分)
△=576(m2-4), yA+yB=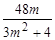 , yAyB=
, yAyB=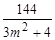 .
.
则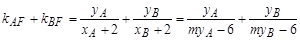
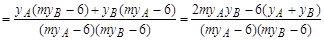 ,
,
而2myAyB-6(yA+yB)=2m·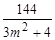 -6·
-6·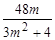 =0, (7分)
=0, (7分)
∴kAF+kBF=0,从而∠AFM=∠BFN.
综合可知:对于任意的割线PAB,恒有∠AFM=∠BFN. (8分)
②方法一:
S△ABF=S△PBF-S△PAF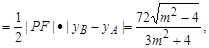 (10分)
(10分)
即S△ABF=
 , (12分)
, (12分)
当且仅当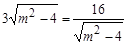 ,即m=±
,即m=± 时(此时适合于△>0的条件)取到等号。
时(此时适合于△>0的条件)取到等号。
∴△ABF面积的最大值是3 . (13分)
. (13分)
方法二: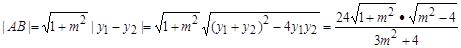
点F到直线AB的距离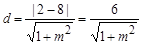 (10分)
(10分)
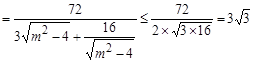 , (12分)
, (12分)
当且仅当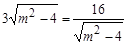 ,即m=±
,即m=± 时取等号。 (13分)
时取等号。 (13分)
考点:直线与圆锥曲线的综合问题;椭圆的标准方程.

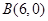 和
和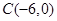 ,过点
,过点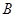 的直线
的直线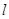 与过点
与过点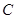 的直线
的直线 相交于点
相交于点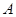 ,设直线
,设直线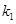 ,直线
,直线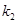 ,如果
,如果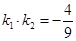 ,求点
,求点 中,
中,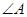 的外角平分线
的外角平分线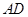 与边
与边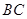 的延长线相交于点
的延长线相交于点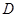 ,则
,则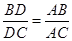 .
.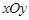 中,已知过点
中,已知过点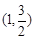 的椭圆
的椭圆 :
: 的右焦点为
的右焦点为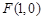 ,过焦点
,过焦点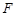 且与
且与 轴不重合的直线与椭圆
轴不重合的直线与椭圆 ,
, 两点,点
两点,点 ,直线
,直线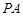 ,
,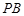 分别交椭圆
分别交椭圆 于
于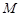 ,
,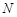 两点.
两点.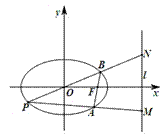
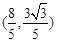 ,试求直线
,试求直线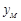 ,
,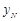 ,试问
,试问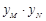 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.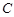 :
: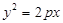 和⊙
和⊙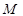 :
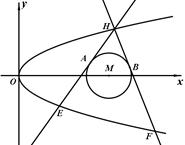
: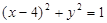 ,过抛物线
,过抛物线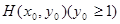 作两条直线与⊙
作两条直线与⊙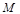 相切于
相切于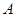 、
、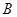 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点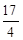 .
.
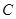 的方程;
的方程;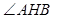 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线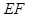 的斜率;
的斜率;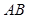 在
在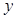 轴上的截距为
轴上的截距为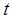 ,求
,求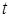 的最小值.
的最小值. 的中心在原点,焦点在
的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为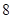 的正方形(记为
的正方形(记为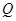 )
) 是直线
是直线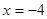 与
与 与椭圆
与椭圆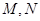 两点,当线段
两点,当线段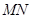 的中点落在正方形
的中点落在正方形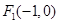 、
、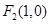 为椭圆
为椭圆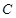 的左、右焦点,且点
的左、右焦点,且点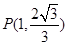 在椭圆
在椭圆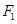 的直线
的直线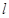 交椭圆
交椭圆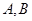 两点,则
两点,则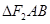 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?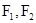 ,椭圆的离心率为
,椭圆的离心率为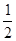 ,且椭圆C经过点
,且椭圆C经过点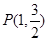 .
.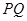 是椭圆过点
是椭圆过点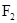 的弦,且
的弦,且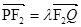 ,求
,求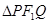 内切圆面积最大时实数
内切圆面积最大时实数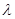 的值.
的值. 、
、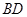 是过抛物线
是过抛物线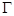 焦点
焦点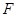 的两条弦,且其焦点
的两条弦,且其焦点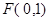 ,
,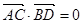 ,点
,点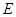 为
为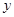 轴上一点,记
轴上一点,记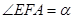 ,其中
,其中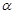 为锐角.
为锐角.
 (
(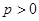 ,
,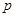 是常数),且动点
是常数),且动点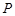 到
到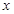 轴的距离比到点
轴的距离比到点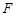 的距离小
的距离小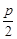 .
. 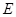 的方程;
的方程; ,若曲线
,若曲线 上存在不同两点
上存在不同两点 、
、 满足
满足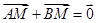 ,求实数
,求实数 时,抛物线
时,抛物线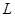 上是否存在异于
上是否存在异于 ,使得经过
,使得经过