题目内容
3.在△ABC中,角A,B,C的对边分别为a,b,c,求证:$\frac{a+b}{c}$=$\frac{cos\frac{A-B}{2}}{sin\frac{C}{2}}$.分析 由正弦定理可得左边=$\frac{a+b}{c}$=$\frac{sinA+sinB}{sinC}$,利用和差化积公式及三角形内角和定理及诱导公式即可得证.
解答 解:左边=$\frac{a+b}{c}$=$\frac{sinA+sinB}{sinC}$=$\frac{2sin\frac{A+B}{2}cos\frac{A-B}{2}}{2sin\frac{A+B}{2}cos\frac{A+B}{2}}$=$\frac{cos\frac{A-B}{2}}{cos\frac{π-C}{2}}$=$\frac{cos\frac{A-B}{2}}{sin\frac{C}{2}}$=右边.
得证.
点评 本题主要考查了正弦定理,和差化积公式,三角形内角和定理及诱导公式的综合应用,属于基本知识的考查.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
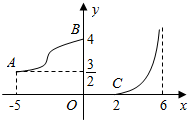 函数f(x)的图象如图所示,其中点O,A,B,C的坐标分别为(0,0),(-5,$\frac{3}{2}$),(0,4),(2,0),则f(-5)=$\frac{3}{2}$,f[f(2)]=4.
函数f(x)的图象如图所示,其中点O,A,B,C的坐标分别为(0,0),(-5,$\frac{3}{2}$),(0,4),(2,0),则f(-5)=$\frac{3}{2}$,f[f(2)]=4.