题目内容
一个五位的自然数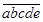 称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中,比40000大的“凸”数的个数是_____.(用数字作答)
称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中,比40000大的“凸”数的个数是_____.(用数字作答)
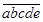 称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中,比40000大的“凸”数的个数是_____.(用数字作答)
称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中,比40000大的“凸”数的个数是_____.(用数字作答) 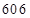
解:因为:由题意知本题是一个分类计数问题,
数字中c的值最小是3,最大是9,
因此需要把c的值进行讨论,
当c=3时,前面两位数字可以从1,2中选只有一种结果,后面两位需要从0,1,2中选两个,共有1×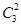 =3种结果,
=3种结果,
当c=4时,前面两位数字可以从1,2,3中选,后面两位需要从0,1,2,3中选两个,共有 ×
×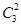 =18种结果
=18种结果
以此类推当c=9时,有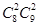
根据分类计数原理知共有在所有的五位数中,比40000大的“凸”数的个数是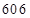
数字中c的值最小是3,最大是9,
因此需要把c的值进行讨论,
当c=3时,前面两位数字可以从1,2中选只有一种结果,后面两位需要从0,1,2中选两个,共有1×
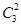 =3种结果,
=3种结果,当c=4时,前面两位数字可以从1,2,3中选,后面两位需要从0,1,2,3中选两个,共有
 ×
×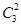 =18种结果
=18种结果以此类推当c=9时,有
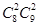
根据分类计数原理知共有在所有的五位数中,比40000大的“凸”数的个数是
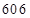

练习册系列答案
相关题目
 种
种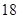 种
种 种
种 种
种
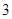 人,女生4人
人,女生4人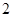 人.
人.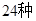
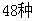
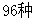
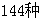
 ,那么
,那么 ____
____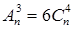 ,则
,则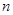 的值为( )
的值为( )