题目内容
设平面区域D是由直线x±2y=0和x=2所围成的三角形（含边界与内部）．若点（x，y）∈D，则目标函数z=x+y的最大值为（ ）
分析：根据平面区域D是由直线x±2y=0和x=2所围成的三角形（含边界与内部），从而得到可行域是图中△ABO及其内部，然后利用直线平移法，即可求得目标函数z=x+y的最大值．
解答：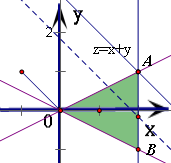
解：平面区域D是由直线x±2y=0和x=2所围成的三角形（含边界与内部），
因此作出三条直线，得可行域是△ABO及其内部（如图）
将直线l：z=x+y，即y=-x+z进行平移，可得
当直线y=-x+z过点A（2，1）时，目标函数z=x+y有最大值
∴zmax=2+1=3．
故选D．
解：平面区域D是由直线x±2y=0和x=2所围成的三角形（含边界与内部），因此作出三条直线，得可行域是△ABO及其内部（如图）
将直线l：z=x+y，即y=-x+z进行平移，可得
当直线y=-x+z过点A（2，1）时，目标函数z=x+y有最大值
∴zmax=2+1=3．
故选D．
点评：本题以简单的线性规划为载体，求目标函数的最大值，属于基础题．
练习册系列答案
相关题目
的两条渐近线和直线
所围成三角形的边界及内部．当
时，
的最大值为（ ）.