题目内容
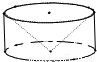
从一个底面半径和高都是
R的圆柱中,挖去一个以圆柱上底面为底,下底面中心为顶点的圆锥,得到如图所示的几何体.如果用一个与圆柱下底面距离等于l并且平行于底面平面去截它,求所得截面的面积.
答案:略
解析:
解析:
|
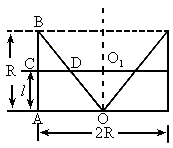
解:轴截面如图,被平行于下底面的平面所截圆柱的截面圆的半径 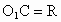 ,圆锥的截面圆的半径 ,圆锥的截面圆的半径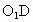 设为x. 设为x.
∵ OA=AB=R,∴△ OAB是等腰直角三角形.又 CD∥OA,则CD=BC.故 x=l.∴截面面积 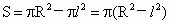
圆柱中挖去圆锥后的几何体被平行于底面的平面所截得的截面是一个圆环面,它是由圆柱被截得的圆面去掉一个圆锥被截得的同心圆面而得.作出轴截面再求解. 处理旋转的有关总是一般要过轴作出轴截面中寻找各元素的关系. |

练习册系列答案
相关题目
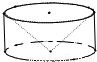
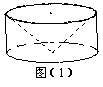
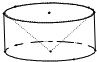 从一个底面半径和高都是R的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图所示的几何体,那么这个几何体的体积是
从一个底面半径和高都是R的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图所示的几何体,那么这个几何体的体积是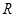 的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.
的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.