题目内容
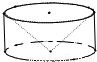
从一个底面半径和高都是R的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图所示的几何体,那么这个几何体的体积是 .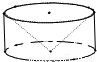
【答案】分析:根据几何体的体积是由圆柱的体积减去圆锥的体积,根据所给的半径和柱体的高,分别求出两种几何体的体积,用圆柱的体积减去圆锥的体积.
解答:解:由题意知,要求的几何体的体积是由圆柱的体积减去圆锥的体积,
圆柱的体积是πR2•R=πR3,
圆锥的体积是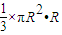 =
=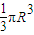 ,
,
∴要求的几何体的体积是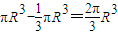 ,
,
故答案为: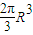 .
.
点评:本题考查旋转体,考查圆柱的体积和圆锥的体积,考查空间简单组合体的结构特征和运算,本题是一个基础题.
解答:解:由题意知,要求的几何体的体积是由圆柱的体积减去圆锥的体积,
圆柱的体积是πR2•R=πR3,
圆锥的体积是
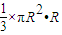 =
=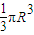 ,
,∴要求的几何体的体积是
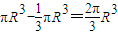 ,
,故答案为:
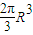 .
.点评:本题考查旋转体,考查圆柱的体积和圆锥的体积,考查空间简单组合体的结构特征和运算,本题是一个基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
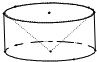 从一个底面半径和高都是R的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图所示的几何体,那么这个几何体的体积是
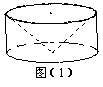
从一个底面半径和高都是R的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图所示的几何体,那么这个几何体的体积是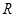 的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.
的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.