题目内容
【题目】已知点![]() 到抛物线
到抛物线![]() 的焦点
的焦点![]() 的距离和它到直线
的距离和它到直线![]() 的距离之比是
的距离之比是![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过圆![]() :
:![]() 上任意一点
上任意一点![]() 作圆的切线
作圆的切线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)求得抛物线的焦点,设![]() ,运用两点的距离公式和点到直线的距离公式,化简整理,可得所求轨迹方程;
,运用两点的距离公式和点到直线的距离公式,化简整理,可得所求轨迹方程;
(2)对直线的斜率讨论,联立直线方程和椭圆方程,运用韦达定理和向量的数量积公式,结合直线与圆相切,即可得到证明.
解:(1)抛物线![]() 的焦点
的焦点![]() ,
,
设![]() ,由题意可得
,由题意可得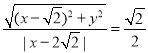 ,
,
两边平方可得![]() ,
,
化为![]() ,
,
点![]() 的轨迹
的轨迹![]() 的方程为椭圆
的方程为椭圆![]() ;
;
(2)证明:当切线![]() 的斜率不存在时切线方程为
的斜率不存在时切线方程为![]() 或
或![]() ,
,
当切线方程为![]() 时,切线与椭圆的两个交点为
时,切线与椭圆的两个交点为![]() 和
和![]() ,
,
此时![]() ,
,
即![]() ;
;
当![]() 时,同理可证得.
时,同理可证得.
当切线![]() 斜率存在时,可设
斜率存在时,可设![]() 的方程为
的方程为![]() ,
,
与椭圆方程联立,可得![]() ,
,
则![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,即
,即![]() .
.
综上可得,![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
【题目】某高校共有10000人,其中男生7500人,女生2500人,为调查该校学生每则平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).调查部分结果如下![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 35 | ||
每周平均体育运动时间超过4小时 | 30 | ||
总计 | 200 |
(1)完成上述每周平均体育运动时间与性别的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 把握认为“该校学生的每周平均体育运动时间与性别有关”;
把握认为“该校学生的每周平均体育运动时间与性别有关”;
(2)已知在被调查的男生中,有5名数学系的学生,其中有2名学生每周平均体育运动时间超过4小时,现从这5名学生中随机抽取2人,求恰有1人“每周平均体育运动时间超过4小时”的概率.
附: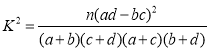 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |