题目内容
![]() (
(![]() 分)
分)![]() 是直角三角形
是直角三角形![]() 斜边
斜边![]() 上的高,(
上的高,(![]() ),
),![]() 分别是
分别是![]() 的内心,
的内心,![]() 的外接圆
的外接圆![]() 分别交
分别交![]() 于
于![]() ,直线
,直线![]() 交于点
交于点![]() ;证明:
;证明:![]() 分别是
分别是![]() 的内心与旁心.
的内心与旁心.
略
解析:
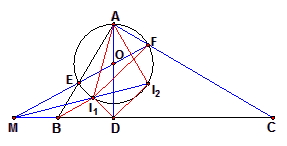
:如图,连![]() ,由
,由![]() ,则圆心
,则圆心![]() 在
在![]() 上,设直径
上,设直径![]() 交
交![]() 于
于![]() ,并简记
,并简记![]() 的三内角为
的三内角为![]() ,由
,由![]()
![]() ,
,
所以![]() ∽
∽![]() ,得
,得![]() ,且
,且![]() ,故
,故![]() ∽
∽![]() ,而
,而![]() ,
,
注意![]() ,
,![]() ,
,
所以![]() ,因此
,因此![]() ,同理得
,同理得![]() ,故
,故![]() 与
与![]() 重合,即圆心
重合,即圆心![]() 在
在![]() 上,而
上,而![]() ,
,
![]() ,所以
,所以![]() 平分
平分![]() ;
;
同理得![]() 平分
平分![]() ,即
,即![]() 是
是![]() 的内心,
的内心,![]() 是
是![]() 的旁心.
的旁心.
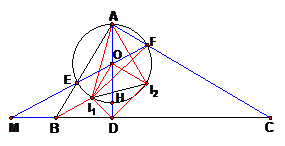 证二:如图,因为
证二:如图,因为![]() ,故
,故![]() 的外接圆圆心
的外接圆圆心![]() 在
在![]() 上,连
上,连![]() ,则由
,则由![]() 为内心知,
为内心知,
![]() , 所以
, 所以
![]() ,
,
于是![]() 四点共圆,所以
四点共圆,所以
![]() ,又因
,又因![]() ,因此点
,因此点![]() 在
在![]() 上,即
上,即![]() 为
为![]() 与
与![]() 的交点.设
的交点.设![]() 与
与![]() 交于另一点
交于另一点![]() ,而由
,而由![]() ,
,
![]() ,可知,
,可知,![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
![]() .因此,点
.因此,点![]() 分别为
分别为![]() 的内心与旁心.
的内心与旁心.

练习册系列答案
相关题目
 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.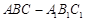 的底面是直角三角形,
的底面是直角三角形,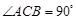 ,侧棱与底面所成角为
,侧棱与底面所成角为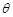 ,点
,点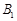 在底面上射影D落在BC上.
在底面上射影D落在BC上.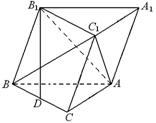
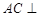 平面
平面 ;
;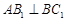 ,求
,求 ,且当
,且当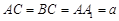 时,求二面角
时,求二面角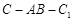 的大小.
的大小.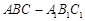 的底面是直角三角形,
的底面是直角三角形,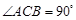 ,侧棱与底面所成角为
,侧棱与底面所成角为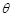 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.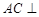 平面
平面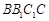 ;
;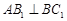 ,求
,求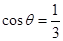 ,且当
,且当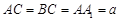 时,求二面角
时,求二面角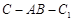 的大小.
的大小.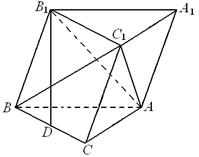
 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.
 平面
平面 ;
; ,求
,求 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小. (Ⅰ)求证:平面
(Ⅰ)求证:平面