题目内容
(本题满分12分)已知斜三棱柱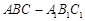 的底面是直角三角形,
的底面是直角三角形,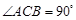 ,侧棱与底面所成角为
,侧棱与底面所成角为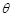 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.
(Ⅰ)求证: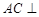 平面
平面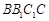 ;
;
(Ⅱ)若点D恰为BC中点,且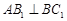 ,求
,求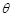 的大小;
的大小;
(III)若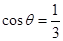 ,且当
,且当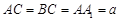 时,求二面角
时,求二面角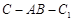 的大小.
的大小.
【答案】
解:(I)∵B1D⊥平面ABC,AC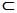 平面ABC,∴
平面ABC,∴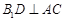
又∵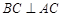 ,
,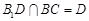 ,∴AC⊥平面
,∴AC⊥平面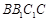
(II)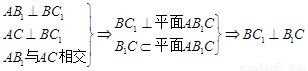
∴四边形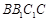 为菱形, 又∵D为BC的中点,
为菱形, 又∵D为BC的中点,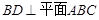
∴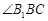 为侧棱和底面所成的角
为侧棱和底面所成的角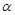 ,∴
,∴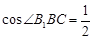
∴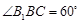 ,即侧棱与底面所成角
,即侧棱与底面所成角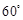 .
.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),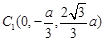 ,平面ABC的法向量
,平面ABC的法向量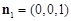 ,设平面ABC1的法向量为
,设平面ABC1的法向量为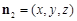 ,
,
由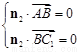 ,即
,即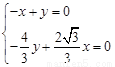 ,
,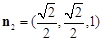
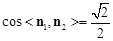 ,
,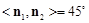
∵二面角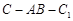 大小是锐二面角,
∴二面角
大小是锐二面角,
∴二面角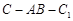 的大小是
的大小是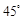 .
.
【解析】略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围