题目内容
已知f(x)=2-|x|,g(x)=x2,设函数h(x)=
.关于h(x)有以下四个判断:
①函数h(x)的图象关于y轴对称;
②函数h(x)在[0,1]上是增函数;
③函数h(x)的值域是[2,+∞);
④当1<m<2时,函数y=h(x)-m的图象与x轴有四个交点.
其中正确判断的序号是
|
①函数h(x)的图象关于y轴对称;
②函数h(x)在[0,1]上是增函数;
③函数h(x)的值域是[2,+∞);
④当1<m<2时,函数y=h(x)-m的图象与x轴有四个交点.
其中正确判断的序号是
①④
①④
.分析:求出函数h(x)的表达式,利用函数h(x)的图象和性质分别进行判断.
解答:解:由f(x)≥g(x),得2-|x|≥x2,即x2+|x|-2≤0,解得-1≤x≤1,
由f(x)<g(x),2-|x|<x2,解得x>1或x<-1,
∴h(x)=
.
作出h(x)的图象如图: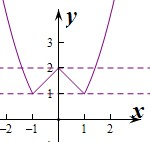
①函数h(x)的图象关于y轴对称,正确.
②函数h(x)在[0,1]上是增函数;正确.
③函数h(x)的值域是[1,+∞);∴③错误.
④由图象可知当1<m<2时,函数y=h(x)与y=m的图象由四个不同的 交点,即函数y=h(x)-m的图象与x轴有四个交点,∴④正确.
故答案为:①④.
由f(x)<g(x),2-|x|<x2,解得x>1或x<-1,
∴h(x)=
|
作出h(x)的图象如图:
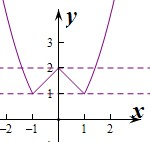
①函数h(x)的图象关于y轴对称,正确.
②函数h(x)在[0,1]上是增函数;正确.
③函数h(x)的值域是[1,+∞);∴③错误.
④由图象可知当1<m<2时,函数y=h(x)与y=m的图象由四个不同的 交点,即函数y=h(x)-m的图象与x轴有四个交点,∴④正确.
故答案为:①④.
点评:本题主要考查分段函数的图象和性质,利用数形结合是解决本题的关键.

练习册系列答案
相关题目