题目内容
已知:如图,AB是圆C:x2+y2+4x-12y+24=0的弦,且过点P(0,5).(Ⅰ)若弦AB的长为
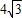 ,求直线AB的方程;
,求直线AB的方程;(Ⅱ)求弦AB中点D的轨迹方程.
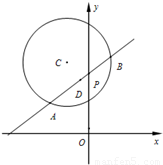
【答案】分析:(Ⅰ)把圆的一般方程化为标准方程求出圆心坐标和圆的半径,解直角三角形求出圆心到直线的距离,设出直线的点斜式方程并整理为一般式,利用点到直线的距离得到k的等式,代入距离后求得k的值;
(Ⅱ)直接设出AB中点D的坐标,把CD⊥PD转化为对应向量的数量积等于0,代入坐标后可得弦AB中点D的轨迹方程.
解答:解:(Ⅰ)设D是线段AB的中点,则CD⊥AB,
由x2+y2+4x-12y+24=0得(x+2)2+(y-6)2=16.
所以圆心C(-2,6),半径r=4.
因为|AB|=4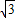 ,∴|AD|=
,∴|AD|=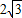 ,又|AC|=4.
,又|AC|=4.
在Rt△ACD中,可得|CD|=2.
设直线l的方程为:y=kx-5,
即kx-y+5=0.由点C到直线AB的距离公式: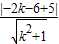 =2,得k=
=2,得k= ,
,
此时直线l的方程为3x-4y+20=0.
又直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
(Ⅱ) 设D(x,y),则CD⊥PD,
∴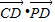 =0,
=0,
∴(x+2,y-6)•(x,y-5)=0,
化简得所求轨迹方程为x2+y2+2x-11y+30=0(在圆内部分).
点评:本题考查了直线与圆的关系,考查了利用平面向量的数量积求轨迹方程,体现了数学转化思想方法,是中档题.
(Ⅱ)直接设出AB中点D的坐标,把CD⊥PD转化为对应向量的数量积等于0,代入坐标后可得弦AB中点D的轨迹方程.
解答:解:(Ⅰ)设D是线段AB的中点,则CD⊥AB,
由x2+y2+4x-12y+24=0得(x+2)2+(y-6)2=16.
所以圆心C(-2,6),半径r=4.
因为|AB|=4
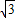 ,∴|AD|=
,∴|AD|=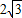 ,又|AC|=4.
,又|AC|=4.在Rt△ACD中,可得|CD|=2.
设直线l的方程为:y=kx-5,
即kx-y+5=0.由点C到直线AB的距离公式:
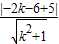 =2,得k=
=2,得k= ,
,此时直线l的方程为3x-4y+20=0.
又直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
(Ⅱ) 设D(x,y),则CD⊥PD,
∴
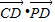 =0,
=0,∴(x+2,y-6)•(x,y-5)=0,
化简得所求轨迹方程为x2+y2+2x-11y+30=0(在圆内部分).
点评:本题考查了直线与圆的关系,考查了利用平面向量的数量积求轨迹方程,体现了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
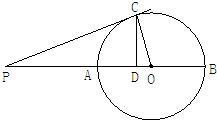 已知:如图,AB是⊙O的直径,点C是⊙O上一点,CD⊥AB,垂足为D,点P在BA的延长线上,且PC是圆O的切线.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,CD⊥AB,垂足为D,点P在BA的延长线上,且PC是圆O的切线. 已知:如图,AB是圆C:x2+y2+4x-12y+24=0的弦,且过点P(0,5).
已知:如图,AB是圆C:x2+y2+4x-12y+24=0的弦,且过点P(0,5).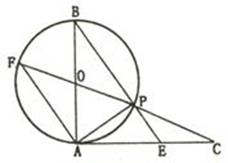
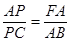
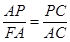
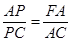 ∵AB=AC
∴
∵AB=AC
∴