题目内容
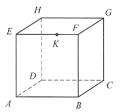
【题目】如图，正方体ABCD－EFGH的一个截面经过顶点A、C及棱EF上一点K，且将正方体分成体积比为3：1的两部分，则
的值为______ .
【答案】
【解析】
记
为截面所在平面,延长AK、BF交于点P，则P在上，故直线CP是与平面BCGF的交线,设CP与FG交于点L，则四边形AKLC为截面,且ABC－KFL为棱台,不妨设正方体棱长为1，则正方体体积为1，设PF=h，则
，由条件知棱台ABC－KFL的体积
，列出方程可得h的值，可得答案.
解：如图，记为截面所在平面.延长AK、BF交于点P，则P在上，故直线CP是与平面BCGF的交线.设CP与FG交于点L，则四边形AKLC为截面.
因平面ABC平行于平面KFL，且AK、BF、CL共点P，故ABC－KFL为棱台.不妨设正方体棱长为1，则正方体体积为1，结合条件知棱台ABC－KFL的体积.
设PF=h，则.
注意到PB、PF分别是棱锥P－ABC与棱锥P－KFL的高，于是
.
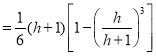
化简得3h2=1，故
.
从而
.
智趣暑假温故知新系列答案
【题目】2019年郑开国际马拉松比赛，于2019年3月31日在郑州、开封举行．某学校本着“我运动，我快乐，我锻炼，我提高”精神，积极组织学生参加比赛及相关活动，为了了解学生的参与情况，从全校学生中随机抽取了150名学生，对是否参与的情况进行了问卷调查，统计数据如下：
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
（1）根据上表说明，能否有97.5%的把握认为参与马拉松赛事与性别有关?
（2）现从参与问卷调查且参与赛事的学生中，采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动，
①求男、女学生各选取多少人；
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍，求恰好选到2名男生的概率．
附：参考公式：
，其中
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
