题目内容
(本小题满分12分)
已知函数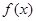 对于任意
对于任意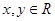 , 总有
, 总有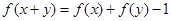 ,
,
并且当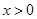 ,
,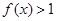
⑴求证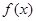 为
为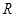 上的单调递增函数
上的单调递增函数
⑵若 ,求解不等式
,求解不等式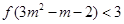
【答案】
(1)见解析;(2)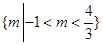 。
。
【解析】本试题主要是考查了运用抽象函数关系式证明函数的单调性,并解不等式。
(1)由定义可设在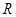 上任取
上任取 ,且
,且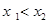
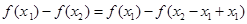
变形得到结论。
(2)因为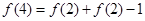
所以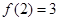 ,然后可知
,然后可知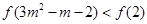 由(1)可知
由(1)可知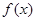 为
为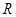 上的单调递增函数,得到
上的单调递增函数,得到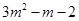
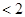 ,解二次不等式得到结论。
,解二次不等式得到结论。
解:(1)在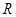 上任取
上任取 ,且
,且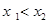
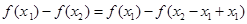
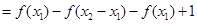
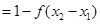
因为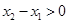 所以
所以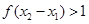
故
即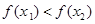
所以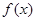 为
为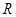 上的单调递增函数---------------------------6分
上的单调递增函数---------------------------6分
(2)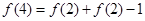
所以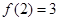 --------------------------8分
--------------------------8分
由此可得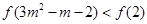 由(1)可知
由(1)可知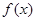 为
为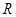 上的单调递增函数
上的单调递增函数
所以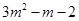
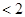 ---------------------10分
---------------------10分
解得: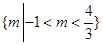 ——-----------------12分
——-----------------12分

练习册系列答案
相关题目