题目内容
(2012•芜湖二模)已知函数f(x)=
(x+
),x≥0,an+1=f(an),对于任意的n∈N*,都有an+1<an.
(Ⅰ)求a1的取值范围;
(Ⅱ)若a1=
,证明an<1+
(n∈N+,n≥2).
(Ⅲ)在(Ⅱ)的条件下证明
+
+…+
-n<
+1.
| 1 |
| 2 |
| 1 |
| x |
(Ⅰ)求a1的取值范围;
(Ⅱ)若a1=
| 3 |
| 2 |
| 1 |
| 2n+1 |
(Ⅲ)在(Ⅱ)的条件下证明
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| 2 |
分析:(Ⅰ)根据函数f(x)的表达式,结合an+1=f(an),解不等式an+1-an<0,再结合an是正数,可得对任意n∈N+,
都有a1>1.
(II)先用导数进行研究,可得函数f(x)在区间(1,+∞)上是增函数.再利用数学归纳的方法,可以证明
出an<1+
(n∈N+,n≥2).
(III)由an+1=f(an)=
(an+
),解出an=an+1+
,再变形得到
-1=
,
结合0<an+1<an得到
-1<
,最后利用g(x)=
在(1,+∞)是增函数,通过放缩得到
-1<
,再以此为依据,进行累加可得原不等式成立.
都有a1>1.
(II)先用导数进行研究,可得函数f(x)在区间(1,+∞)上是增函数.再利用数学归纳的方法,可以证明
出an<1+
| 1 |
| 2n+1 |
(III)由an+1=f(an)=
| 1 |
| 2 |
| 1 |
| an |
| an+12-1 |
| an |
| an+1 |
1-
|
结合0<an+1<an得到
| an |
| an+1 |
1-
|
1-
|
| an |
| an+1 |
|
解答:解:(Ⅰ)∵f(an)=
(an+
), an>0
∴an+1-an=
(an+
)-an=
(
-an)<0
∴
•
<0
∵an是正数,
∴an>1对任意n∈N+恒成立,因此a1>1.
(II)∵f/(x) =
(x+
)/=
∴当x>1时,f′(x)>0,函数f(x)在区间(1,+∞)上是增函数
下面用数学归纳法,证明an<1+
(n∈N+,n≥2).
①当n=2时,由a1=
,得a2=
(a1+
)=
<1+
=
②设当n=k时,ak<1+
成立
则当n=k+1时,ak+1=f(an)<f(1+
)=
(1+
+
)
=
(1+
+1-
)<
(2+
)=1+
,不等式也成立
综合①②可得,对任意的n∈N+,n≥2),均有an<1+
成立.
(III)an+1=
(an+
)⇒an=an+1+
⇒
=1+
⇒
-1=
<
设g(x)=
,则g(x)在(1,+∞)是增函数
∴
-1<
<
=
<
<
又∵
-1=
<
∴
+
+…+
-n<
+
+
+…+
=
=(
+1) [1-(
)n] <
+1
即对任意的n∈N+,n≥2,均有
+
+…+
-n<
+1成立.
| 1 |
| 2 |
| 1 |
| an |
∴an+1-an=
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| an |
∴
| 1 |
| 2 |
| 1-an2 |
| an |
∵an是正数,
∴an>1对任意n∈N+恒成立,因此a1>1.
(II)∵f/(x) =
| 1 |
| 2 |
| 1 |
| x |
| x2-1 |
| 2x2 |
∴当x>1时,f′(x)>0,函数f(x)在区间(1,+∞)上是增函数
下面用数学归纳法,证明an<1+
| 1 |
| 2n+1 |
①当n=2时,由a1=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| a1 |
| 13 |
| 12 |
| 1 |
| 23 |
| 9 |
| 8 |
②设当n=k时,ak<1+
| 1 |
| 2k+1 |
则当n=k+1时,ak+1=f(an)<f(1+
| 1 |
| 2k+1 |
| 1 |
| 2 |
| 1 |
| 2k+1 |
| 1 | ||
1+
|
=
| 1 |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 1+2k+1 |
| 1 |
| 2 |
| 1 |
| 2 k+1 |
| 1 |
| 2 (k+1)+1 |
综合①②可得,对任意的n∈N+,n≥2),均有an<1+
| 1 |
| 2n+1 |
(III)an+1=
| 1 |
| 2 |
| 1 |
| an |
| an+12-1 |
⇒
| an |
| an+1 |
1-
|
| an |
| an+1 |
1-
|
1-
|
设g(x)=
1-
|
∴
| an |
| an+1 |
1-
|
1-
|
|
|
|
又∵
| a1 |
| a2 |
| 5 |
| 13 |
|
∴
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
|
|
|
|
| ||||||||
1-
|
=(
| 2 |
| ||
| 2 |
| 2 |
即对任意的n∈N+,n≥2,均有
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| 2 |
点评:本题综合考查了函数的单调性、函数与方程、数列的递推关系、等比数列的求和公式和运用放缩法证明不等式等知识点,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
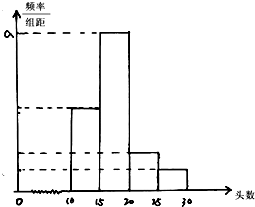 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: