题目内容
 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为| 7 |
(1)求证:BC∥EF;
(2)若四边形ABCD是正方形,求证BC⊥BE;
(3)在(2)的条件下,求二面角A-BC-E的平面角的一个三角函数值.
分析:(1)由圆柱的性质知:AD平行平面BCFE,又过AD作圆柱的截面交下底面于BC.AD∥BC,由此能够证明BC∥EF.
(2)由四边形ABCD是正方形,知BC⊥AB,又AE⊥BC,由此能够证明BC⊥BE.
(3)设正方形ABCD的边长为x,则在Rt△AEB中有:BE2=x2-4在Rt△FEB中有:BE2+x2=28,由此能够求出二面角A-BC-E的平面角的一个三角函数值.
(2)由四边形ABCD是正方形,知BC⊥AB,又AE⊥BC,由此能够证明BC⊥BE.
(3)设正方形ABCD的边长为x,则在Rt△AEB中有:BE2=x2-4在Rt△FEB中有:BE2+x2=28,由此能够求出二面角A-BC-E的平面角的一个三角函数值.
解答:证明:(1)由圆柱的性质知:AD平行平面BCFE
又过AD作圆柱的截面交下底面于BC.AD∥BC…..(2分)
又AE、DF是圆柱的两条母线AE∥DF,且AE=DF,
∴四边形ADFE是平行四边形AD∥EF,
∴BC∥EF….(4分)
(2)∵四边形ABCD是正方形,
∴BC⊥AB,又AE⊥BC,
BE、AE是平面ABE内两条相交直线,
∴BC⊥平面ABE…(9分)
∴BC⊥BE…(10分)
(3)设正方形ABCD的边长为x,
则在Rt△AEB中有:BE2=x2-4
在Rt△FEB中有:BE2+x2=28
∴x=4…(12分)
由(2)可知:∠ABE为二面角A-BC-E的平面角,
所以sin∠ABE=
=
…(14分)
又过AD作圆柱的截面交下底面于BC.AD∥BC…..(2分)
又AE、DF是圆柱的两条母线AE∥DF,且AE=DF,
∴四边形ADFE是平行四边形AD∥EF,
∴BC∥EF….(4分)
(2)∵四边形ABCD是正方形,
∴BC⊥AB,又AE⊥BC,
BE、AE是平面ABE内两条相交直线,
∴BC⊥平面ABE…(9分)
∴BC⊥BE…(10分)
(3)设正方形ABCD的边长为x,
则在Rt△AEB中有:BE2=x2-4
在Rt△FEB中有:BE2+x2=28
∴x=4…(12分)
由(2)可知:∠ABE为二面角A-BC-E的平面角,
所以sin∠ABE=
| AE |
| AB |
| 1 |
| 2 |
点评:本题考查异面直线的平行的证明,考查直线与直线垂直的证明,考查二面角的平面角的三角函数值的计算,解题时要认真审题,仔细解答,合理地化空间问题为平面问题.

练习册系列答案
相关题目
 (2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
(2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点. (2013•广州三模)如图所示,圆柱的高为2,底面半径为
(2013•广州三模)如图所示,圆柱的高为2,底面半径为 (2012•韶关一模)如图所示,圆柱的高为2,底面半径为
(2012•韶关一模)如图所示,圆柱的高为2,底面半径为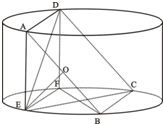 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为