Question

（2012•汕头二模）如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABEFD．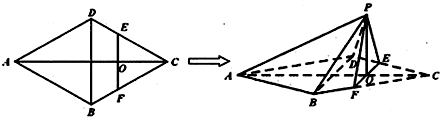
（1）求证：BD⊥平面POA；
（2）记三棱锥P-ABD体积为V₁，四棱锥P-BDEF体积为V₂，且

V1

V2

=

4

3

，求此时线段PO的长．

Answer 1

分析：（1）根据EF⊥AC得PO⊥EF，由平面PEF⊥平面ABEFD结合面面垂直的性质定理，证出PO⊥平面ABEFD，从而得到PO⊥BD．由此结合AO⊥BD，利用线面垂直判定定理即可证出BD⊥平面POA；
（2）由PO⊥平面ABEFD，得PO是三棱锥P-ABD和四棱锥P-BDEF的高，因此将

V1

V2

=

4

3

化简可得S_△ABD=

4

3

S_{四边形BDEF}，从而得到S_△CEF=

1

4

S_△BCD．最后根据△CEF∽△CDB，利用面积比等于相似比的平方，结合菱形ABCD中有关数据即可算出此时线段PO的长等于

3

．

解答：解：（1）∵在菱形ABCD中，BD⊥AC，∴AO⊥BD
∵EF⊥AC，∴PO⊥EF
∵平面PEF⊥平面ABEFD，平面PEF∩平面ABEFD=EF，PO?平面PEF
∴PO⊥平面ABEFD，结合BD?平面ABEFD，可得PO⊥BD
∵AO⊥BD，且AO、PO是平面POA内的相交直线
∴BD⊥平面POA；
（2）设AO、BO相交于点H，由（1）得PO⊥平面ABEFD，
∴PO是三棱锥P-ABD和四棱锥P-BDEF的高
∴V₁=

1

3

S_△ABD•PO，V₂=

1

3

S_{四边形BDEF}•PO，
∵

V1

V2

=

4

3

，可得S_△ABD=

4

3

S_{四边形BDEF}，
∴S_{四边形BDEF}=

3

4

S_△ABD=

3

4

S_△BCD，可得S_△CEF=

1

4

S_△BCD．
∵BD⊥AC，EF⊥AC，EF∥BD，∴△CEF∽△CDB，
因此，(

CO

CH

)2=

S△CEF

S△BCD

=

1

4

，可得CO=

1

2

CH=

1

2

AH
∵菱形ABCD中，边长为4且∠DAB=60°
∴△ABD是边长为4的正三角形，得AH=

3

2

×4=2

3

，从而得到CO=

1

2

×2

3

=

3

∴此时线段PO的长等于

3

．

点评：本题给出平面折叠问题，求证BD⊥平面POA，并在已知三棱锥P-ABD体积与四棱锥P-BDEF体积比的情况下求线段PO的长．着重考查了线面垂直的判定与性质、锥体的体积公式和运用三角形相似求线段比值等知识，属于中档题．