题目内容
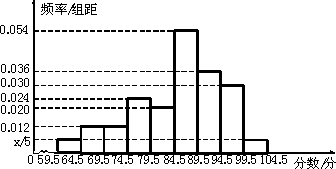
 为了解某校学生数学竞赛的成绩分布,从该校参加数学竞赛的学生成绩中抽取一个样本,并分成5组,绘成频率分布直方图如图,从左到右各小组的小长方形的高之比为1:2:2:20:5,最右边一组的频数是20,请结合直方图的信息,解答下列问题;
为了解某校学生数学竞赛的成绩分布,从该校参加数学竞赛的学生成绩中抽取一个样本,并分成5组,绘成频率分布直方图如图,从左到右各小组的小长方形的高之比为1:2:2:20:5,最右边一组的频数是20,请结合直方图的信息,解答下列问题;(Ⅰ)样本容量是多少?
(Ⅱ)现用分层抽样的方法在该样本中抽取30个学生的成绩作进一步调查,问成绩在120分到150分的学生有几个?
(Ⅲ)已知成绩在120分到150分的学生中,至少有5个是男生,求成绩在120分到150分的学生中,男生比女生多的概率.
分析:(I)利用频率分布直方图中,小矩形的高之比=面积之比=频率之比,而
=频率,代入数据计算可求;
(II)根据频率之比,可求成绩在120分到150分的学生数,算出分层抽样的抽取比例,乘以抽取人数,可得应从成绩在120分到150分的学生中抽取的人数;
(III)用列举法求出基本事件数和男生比女生多的基本事件数,代入古典概型概率公式计算.
| 频数 |
| 样本容量 |
(II)根据频率之比,可求成绩在120分到150分的学生数,算出分层抽样的抽取比例,乘以抽取人数,可得应从成绩在120分到150分的学生中抽取的人数;
(III)用列举法求出基本事件数和男生比女生多的基本事件数,代入古典概型概率公式计算.
解答:解:(Ⅰ)设样本容量为n,由题意得
=
,所以n=120
所以样本的容量为120;
(Ⅱ)由小长方形的高之比为1:2:2:20:5,得小长方体的面积之比(频率之比)为1:2:2:20:5,
∴成绩在120分到150分的学生有
×120=80,则分层抽样抽取的比例
,
∴抽取30个学生应从成绩在120分到150分的学生中抽取
×30=20人;
(Ⅲ)设成绩在120分到150分的学生中,男生比女生多的事件记为A,男生数与女生数记为数对(x,y),
则基本事件有:(5,15),(6,14),(7,13),(8,12),(9,11),(10,10),(11,9),
(12,8),(13,7),(14,6),(15,5),(16,4),(17,3),(18,2),(19,1),(20,0)共16对,
而事件A包含的事件有:(11,9),(12,8),(13,7),(14,6),(15,5),
(16,4),(17,3),(18,2),(19,1),(20,0)共10对.
∴P(A)=
=
.
| n |
| 1+2+2+20+5 |
| 20 |
| 5 |
所以样本的容量为120;
(Ⅱ)由小长方形的高之比为1:2:2:20:5,得小长方体的面积之比(频率之比)为1:2:2:20:5,
∴成绩在120分到150分的学生有
| 20 |
| 30 |
×120=80,则分层抽样抽取的比例
| 80 |
| 120 |
∴抽取30个学生应从成绩在120分到150分的学生中抽取
| 80 |
| 120 |
(Ⅲ)设成绩在120分到150分的学生中,男生比女生多的事件记为A,男生数与女生数记为数对(x,y),
则基本事件有:(5,15),(6,14),(7,13),(8,12),(9,11),(10,10),(11,9),
(12,8),(13,7),(14,6),(15,5),(16,4),(17,3),(18,2),(19,1),(20,0)共16对,
而事件A包含的事件有:(11,9),(12,8),(13,7),(14,6),(15,5),
(16,4),(17,3),(18,2),(19,1),(20,0)共10对.
∴P(A)=
| 10 |
| 16 |
| 5 |
| 8 |
点评:本题考查了分层抽样方法,频率分布直方图,考查了古典概型的概率计算,列举法求基本事件个数是求古典概型概率的基本方法.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
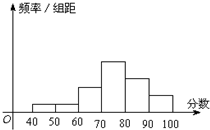 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.请结合直方图的信息,解答下列问题:
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.请结合直方图的信息,解答下列问题: