题目内容
求函数f（x）=2x3+3x2-12x+1的极值．
分析：函数f（x）在区间（a，b）内某一点x0取得极值的充要条件是函数在这一点附近的导数异号且f′（x0）=0．
解答：解：∵函数f（x）=2x3+3x2-12x+1，
∴f′（x）=6x2+6x-12=6（x+2）（x-1），
令f′（x）=0，解得x=-2，或1．
列表如下：
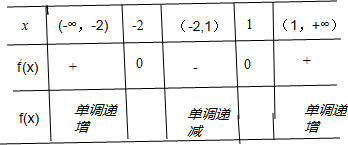
由表可知：当x=-2时，函数f（x）取得极大值，且f（-2）=2×（-2）3+3×（-2）2-12×（-2）+1=21；
当x=1时，函数f（x）取得极小值，且f（1）=2+3-12+1=-6．
∴f′（x）=6x2+6x-12=6（x+2）（x-1），
令f′（x）=0，解得x=-2，或1．
列表如下：
由表可知：当x=-2时，函数f（x）取得极大值，且f（-2）=2×（-2）3+3×（-2）2-12×（-2）+1=21；
当x=1时，函数f（x）取得极小值，且f（1）=2+3-12+1=-6．
点评：掌握函数取得极值的充要条件是解题的关键．
练习册系列答案
相关题目
（2012•湖南模拟）选做题（请考生在第16题的三个小题中任选两题作答，如果全做，则按前两题记分，要写出必要的推理与演算过程）