题目内容

函数f(x)=x|x|+bx+c，给出四个命题：

①当C＝0时，y＝f(x)是奇函数；

②当b=0，c>0时方程f(x)＝0只有一个实数根；

③y＝f(x)的图象关于点(0,c)对称；

④方程f(x)=0至多有两个实数根.

上述命题中，所有正确命题的序号是________.

 

【答案】

①②③

【解析】

试题分析：①当时，的定义域是R，且有，所以是奇函数正确；

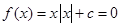②当时，知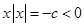只有一个负数解，正确；

③点在函数图像上，那么，即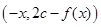也在函数图像上，所以函数图像关于点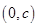对称正确；

④例如方程的根为1,2，有三个实数根，错误.

考点：二次函数的图像与性质.

 

练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
已知三次函数f（x）的导函数f′（x）=3x2-3ax，f（0）=b，a、b为实数．
（1）若曲线y=f（x）在点（a+1，f（a+1））处切线的斜率为12，求a的值；
（2）若f（x）在区间[-1，1]上的最小值、最大值分别为-2、1，且1＜a＜2，求函数f（x）的解析式．
探究函数f（x）=x+
4
x
，x∈（0，+∞）的最小值，并确定取得最小值时x的值．列表如下：
x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
y … 8.5 5 4.17 4.05 4.005 4 4.005 4.02 4.04 4.3 5 5.8 7.57 …
请观察表中值y随x值变化的特点，完成以下的问题．
函数f（x）=x+
4
x
（x＞0）在区间（0，2）上递减；
函数f（x）=x+
4
x
（x＞0）在区间
（2，0）
（2，0）
上递增．
当x=
2
2
时，y最小=
4
4
．
证明：函数f（x）=x+
4
x
（x＞0）在区间（0，2）递减．
思考：（直接回答结果，不需证明）
（1）函数f（x）=x+
4
x
（x＜0）有没有最值？如果有，请说明是最大值还是最小值，以及取相应最值时x的值．
（2）函数f（x）=ax+
b
x
，（a＜0，b＜0）在区间
[-
b
a
，0）
[-
b
a
，0）
 和
（0，
b
a
]
（0，
b
a
]
上单调递增．
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网