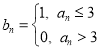题目内容
【题目】如图(1),在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点.以
中点.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图(2).
的位置,如图(2).
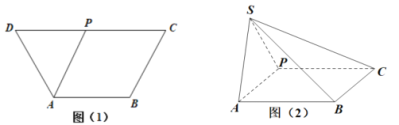
(1)求证:![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2)![]()
【解析】
(1)根据已知的长度和平行关系可证得![]() 均为等边三角形,取
均为等边三角形,取![]() 中点
中点![]() ,根据等腰三角形三线合一性质可证得
,根据等腰三角形三线合一性质可证得![]() ,
,![]() ,则根据线面垂直判定定理证得
,则根据线面垂直判定定理证得![]() 平面
平面![]() ,由线面垂直性质定理可得结论;
,由线面垂直性质定理可得结论;
(2)利用体积桥的方式![]() 可构造出关于所求距离的方程,解方程求得结果.
可构造出关于所求距离的方程,解方程求得结果.
(1)在图![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点
中点
![]() 四边形
四边形![]() 是菱形,且
是菱形,且![]() 是等边三角形,即图
是等边三角形,即图![]() 中
中![]() 是等边三角形
是等边三角形
连结![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
则![]() ,即
,即![]() 是等边三角形/span>
是等边三角形/span>
设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
(2)由(1)知:![]()
又![]()
![]()
![]()
又![]() ,
,![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,即
,即![]() 为三棱锥
为三棱锥![]() 的高
的高
设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
在![]() 中,
中,![]() ,
,![]()
![]()
由![]() 得:
得:![]() ,解得:
,解得:![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]()

【题目】重庆市的新高考模式为“![]() ”,其中“3”是指语文、数学、外语三门必步科目:“1”是指物理、历史两门科目必选且只选一门;“2”是指在政治、地理、化学、生物四科中必须任选两门,这样学生的选科就可以分为两类:物理类与历史类,比如物理类有:物理+化学+生物,物理+化学+地理,物理+化学+政治.物理+政治+地理,物理+政治+生物,物理+生物+地理.重庆某中学高一学生共1200人,其中男生650人,女生550人,为了适应新高考,该校高一的学生在3月份进行了“
”,其中“3”是指语文、数学、外语三门必步科目:“1”是指物理、历史两门科目必选且只选一门;“2”是指在政治、地理、化学、生物四科中必须任选两门,这样学生的选科就可以分为两类:物理类与历史类,比如物理类有:物理+化学+生物,物理+化学+地理,物理+化学+政治.物理+政治+地理,物理+政治+生物,物理+生物+地理.重庆某中学高一学生共1200人,其中男生650人,女生550人,为了适应新高考,该校高一的学生在3月份进行了“![]() ”的选科,选科情况部分数据如下表所示:(单位:人)
”的选科,选科情况部分数据如下表所示:(单位:人)
性别 | 物理类 | 历史类 | 合计 |
男生 | 590 | ||
女生 | 240 | ||
合计 | 900 |
(1)请将题中表格补充完整,并判断能否有99%把握认为“是否选择物理类与性别有关”?
(2)已知高一9班和10班选科结果都只有四种组合:物理+化学+生物,物理+化学+地理,政治+历史+地理,政治+历史+生物.现用数字1,2,3,4依次代表这四种组合,两个班的选科数据如下表所示(单位:人).
理化生 | 理化地 | 政史地 | 政史生 | 班级总人数 | |
9班 | 18 | 18 | 12 | 12 | 60 |
10班 | 24 | 12 | 18 | 6 | 60 |
现分别从两个班各选一人,记他们的选科结果分别为![]() 和
和![]() ,令
,令![]() ,用频率代表概率,求随机变量
,用频率代表概率,求随机变量![]() 的分布列和期望.(参考数据:
的分布列和期望.(参考数据:![]() ,
,![]() ,
,![]() )
)
附: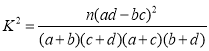 ;
;
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【题目】九龙坡区围绕大力发展高新技术产业、推进高质量城市管理、创造高品质人民生活,建设宜居、宜业、宜游的“三高九龙坡、三宜山水城”的总愿景,全面开启新时代的新梦想、新征程.热心网友“我是坡民”通过问卷,对近五年游客满意度排在前三名的区内景点进行了统计,结果如表一.根据此表,他又对游览过热门景点重庆动物园的100名游客进行满意度调查,给景点打分,满分为100分,得分超过90分的为“特别满意”,其余为“基本满意”,将受调查游客年龄为12岁及以下的人群称为儿童,得到![]() 列联表,如表二:
列联表,如表二:
表一:
年份景点排名 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
1 | 重庆动物园 | 重庆动物园 | 龙门阵景区 | 彩云湖 | 彩云湖 |
2 | 华岩景区 | 华岩景区 | 重庆动物园龙 | 龙门阵景区 | 黄桷坪涂鸦街 |
3 | 巴国城 | 海兰云天 | 黄桷坪涂鸦街 | 华岩景区 | 重庆动物园 |
表二:
特别满意 | 基本满意 | 合计 | |
儿童 | 40 | ||
非儿童 | 30 | ||
合计 | 60 | 100 |
(1)完成表二的列联表,并判断是否有99.9%的把握认为调查对象是否“特别满意”与是否是儿童有关;
(2)为安排节假日出行,“我是坡民”从表一的5个年份中随机选择2个年份,再从这2个年份排名前三的景点中任意选择1个景点,记选择出的景点中“重庆动物园”出现的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名,其评估成绩![]() 近似的服从正态分布
近似的服从正态分布![]() .现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
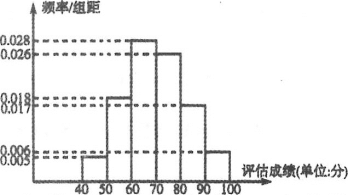
(1)求样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若学校规定评估成绩超过![]() 分的毕业生可参加
分的毕业生可参加![]() 三家公司的面试.
三家公司的面试.
(ⅰ)用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
(ⅱ)若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为![]() ,李华准备依次从
,李华准备依次从![]() 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择
三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择![]() 公司的哪些岗位?
公司的哪些岗位?
并说明理由.
附:![]() ,若随机变量
,若随机变量![]() ,
,
则![]() .
.