题目内容
数列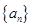 的通项公式是
的通项公式是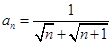 ,若前n项和为10,则项数
,若前n项和为10,则项数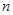 为( )
为( )
| A.11 | B.99 | C.120 | D.121 |
C
解析试题分析:根据通项公式的特点,可选择不同的求和方法,常用的有列项相消法,错位相减法,分组求和法,奇偶并项求和法, ∴
∴
考点:裂项相消法求数列的前n项和.

练习册系列答案
相关题目
设等差数列 的前n项和为
的前n项和为 ,若
,若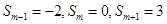 ,则
,则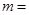 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
数列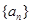 的通项公式为
的通项公式为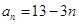 ,
,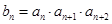 ,
,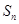 是数列
是数列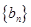 的前
的前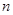 项和,则
项和,则 的最大值为( )
的最大值为( )
| A.280 | B.300 | C.310 | D.320 |
已知等差数列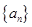 满足
满足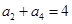 ,
, 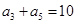 ,则它的前10项和
,则它的前10项和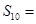 ( )
( )
| A.85 | B.135 | C.95 | D.23 |
公差不为零的等差数列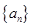 的前
的前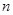 项和为
项和为 ,若
,若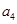 是
是 与
与 的等比中项,且
的等比中项,且 ,则
,则 =( )
=( )
| A.80 | B.160 | C.320 | D.640 |
在一列数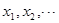 中,已知
中,已知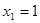 ,且当
,且当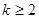 时,
时,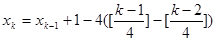 ,其中,
,其中,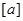 表示不超过实数
表示不超过实数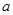 的最大整数(如
的最大整数(如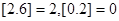 )则
)则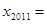 ( )
( )
A.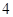 | B.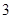 | C.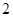 | D. |
在数列{an}中,已知a1 = 2,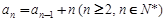 ,则a4等于( )
,则a4等于( )
| A.4 | B.11 | C.10 | D.8 |
定义:数列 ,满足
,满足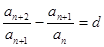
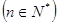 d为常数,我们称
d为常数,我们称 为等差比数列,已知在等差比数列
为等差比数列,已知在等差比数列 中,
中,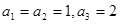 ,则
,则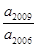 的个位数( )
的个位数( )
| A.3 | B.4 | C.6 | D.8 |
 和
和 满足:
满足: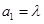 ,
,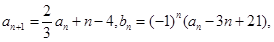 其中
其中 为实数,
为实数,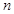 为正整数.
为正整数. ;
;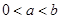 ,是否存在实数
,是否存在实数 成立? 若存在,求
成立? 若存在,求