题目内容
定义:数列 ,满足
,满足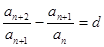
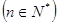 d为常数,我们称
d为常数,我们称 为等差比数列,已知在等差比数列
为等差比数列,已知在等差比数列 中,
中,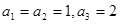 ,则
,则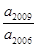 的个位数( )
的个位数( )
| A.3 | B.4 | C.6 | D.8 |
C
解析试题分析:由题意可知: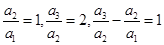 .∴数列{
.∴数列{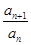 }为以1为首项以1为公差的等差数列.∴
}为以1为首项以1为公差的等差数列.∴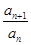 =1+(n-1)1=n.n∈N*∴
=1+(n-1)1=n.n∈N*∴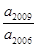 =2006.所以
=2006.所以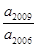 的末位数字是6.故选C.
的末位数字是6.故选C.
考点:本题考查了数列的新定义问题.
点评:在解答的过程当中充分体现了新定义的知识、等比数列的知识以及数据的观察和处理能力.值得同学们体会和反思

练习册系列答案
相关题目
数列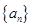 的通项公式是
的通项公式是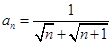 ,若前n项和为10,则项数
,若前n项和为10,则项数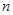 为( )
为( )
| A.11 | B.99 | C.120 | D.121 |
数列{a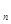 }中,a
}中,a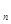 =
=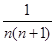 ,前n项和为
,前n项和为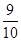 ,则项数n为
,则项数n为
| A.12 | B.11 | C.10 | D.9 |
已知数列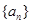 中,
中,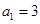 ,
,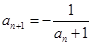 (
(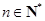 ),能使
),能使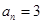 的
的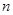 可以等于( ).
可以等于( ).
A.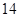 | B.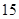 | C. | D. |
已知各项均不为零的数列{an},定义向量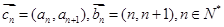 .下列命题中真命题是
.下列命题中真命题是
A.若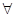 n∈N*总有 n∈N*总有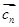 ∥ ∥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
B.若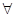 n∈N*总有 n∈N*总有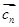 ∥ ∥ 成立,则数列{an}是等比数列; 成立,则数列{an}是等比数列; |
C.若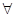 n∈N*总有 n∈N*总有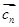 ⊥ ⊥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
D.若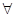 n∈N*总有 n∈N*总有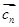 ⊥ ⊥ 成立,则数列{an}是等比数列. 成立,则数列{an}是等比数列. |
已知函数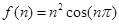 ,且
,且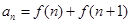 ,则
,则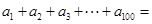 ( )
( )
| A.0 | B.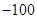 | C.100 | D.10200 |
等差数列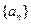 中,
中,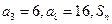 是数列
是数列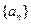 的前n项和,若
的前n项和,若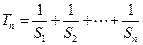 ,则
,则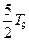 最接近的整数是 ( )
最接近的整数是 ( )
| A.5 | B.4 | C.2 | D.1 |
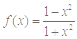 ,则
,则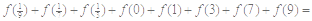 .
.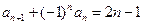 ,则{an}的前
,则{an}的前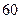 项和为
项和为