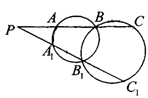
题目内容
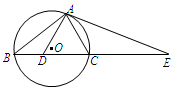
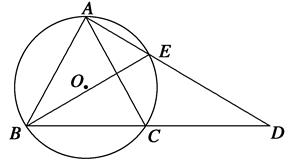
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连结AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
（1）见解析；
（2）见解析．
（2）见解析．
(1)由直线CD与⊙O相切,得∠CEB=∠EAB.
由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=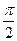
;
又EF⊥AB,得∠FEB+∠EBF=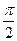,从而∠FEB=∠EAB.
故∠FEB=∠CEB.
(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,
得Rt△BCE≌Rt△BFE,所以BC=BF.
类似可证:Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,
所以EF2=AD·BC.
由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=
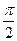;又EF⊥AB,得∠FEB+∠EBF=
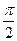,从而∠FEB=∠EAB.故∠FEB=∠CEB.
(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,
得Rt△BCE≌Rt△BFE,所以BC=BF.
类似可证:Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,
所以EF2=AD·BC.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
AD，N是AB的中点，NF⊥CE于F，求证：FN2＝EF·FC.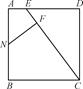
__________
、
，直线
与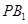
分别与两圆交于点
、
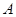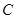和
、
，
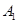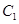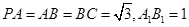，则
.