题目内容
【题目】已知二次函数f(x)的对称轴x=﹣2,f(x)的图象被x轴截得的弦长为2 ![]() ,且满足f(0)=1.
,且满足f(0)=1.
(1)求f(x)的解析式;
(2)若f(( ![]() )x)>k,对x∈[﹣1,1]恒成立,求实数k的取值范围.
)x)>k,对x∈[﹣1,1]恒成立,求实数k的取值范围.
【答案】
(1)解:∵二次函数f(x)的对称轴x=﹣2,∴f(x)=a(x+2)2+k(a≠0),
又f(0)=1,∴4a+k=1…①
又∵二次函数f(x)的对称轴x=﹣2,且f(x)的图象被x轴截得的弦长为2 ![]() ,∴f(x)过点(﹣2+
,∴f(x)过点(﹣2+ ![]() ,0),
,0),
∴3a+k=0…②,
由①②式得 a=1,k=﹣3
∴f(x)的解析式为:f(x)=(x+2)2﹣3
(2)解:f(( ![]() )x)>k,对x∈[﹣1,1]恒成立[(
)x)>k,对x∈[﹣1,1]恒成立[( ![]() )x+2]2﹣3>k,对x∈[﹣1,1]恒成立,
)x+2]2﹣3>k,对x∈[﹣1,1]恒成立,
∴k+3<([( ![]() )x+2]2)min.当x∈[﹣1,1]时,
)x+2]2)min.当x∈[﹣1,1]时, ![]() ,∴([(
,∴([( ![]() )x+2]2)min=
)x+2]2)min= ![]() ,
,
k+3< ![]() k<
k< ![]() ,∴实数k的取值范围:(﹣∞,
,∴实数k的取值范围:(﹣∞, ![]() )
)
【解析】(1)设f(x)=a(x+2)2+k(a≠0),由弦长为2 ![]() ,f(0)=1可得a和k,从而可求得f(x)的解析式;(2)f((
,f(0)=1可得a和k,从而可求得f(x)的解析式;(2)f(( ![]() )x)>k,对x∈[﹣1,1]恒成立k+3<([(
)x)>k,对x∈[﹣1,1]恒成立k+3<([( ![]() )x+2]2)min
)x+2]2)min
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】已知椭圆E: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
. 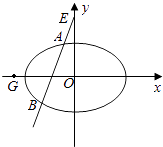
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() ,其中
,其中![]() )
)