题目内容
某球与一个120°的二面角的两个面相切于A、B两点，且A、B两点间的球面距离为π，则此球的表面积是（ ）
| A、12π | B、24π | C、36π | D、144π |
分析：画出图形，圆O是球的一个大圆，∠MAN是二面角的平面角，AM、AN是圆O的切线，欲求两切点间的球面距离即求圆O中劣弧 MN^的长，将立体几何问题转化为平面几何问题解决．
解答：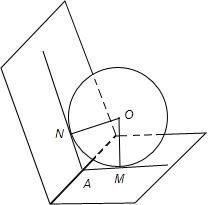
解：画出图形，如图，在四边形OMNA中，AM、AN是球的大圆的切线，
∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是 MN^=
×OM=π．
∴OM=3，则此球的表面积是36π
故选C．
解：画出图形，如图，在四边形OMNA中，AM、AN是球的大圆的切线，∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是 MN^=
| π |
| 3 |
∴OM=3，则此球的表面积是36π
故选C．
点评：空间几何体的主要元素往往集中在某一特征截面上，这个特征截面是一个平面图，从而将立体几何问题转化为平面几何问题．从特征截面入手加以剖析，实现转化是解题的关键．
练习册系列答案
相关题目