题目内容
已知函数 .
.
(1)解不等式 ;
;
(2)若 ,求证:
,求证:
(1)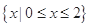 (2)见试题解析
(2)见试题解析
解析试题分析:(1)先将不等式 具体化为
具体化为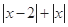
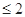 ,通过分类讨论去掉绝对值转化为一元一次不等式组,通过解不等式组即可解出本不等式的解;(2)先将
,通过分类讨论去掉绝对值转化为一元一次不等式组,通过解不等式组即可解出本不等式的解;(2)先将 具体化,观察所证不等式的特点,利用绝对不等式性质即可证明所要证明的不等式.
具体化,观察所证不等式的特点,利用绝对不等式性质即可证明所要证明的不等式.
试题解析:(1)∵
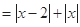 . 1分
. 1分
因此只须解不等式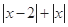
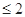 . 2分
. 2分
当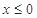 时,原不式等价于
时,原不式等价于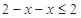 ,即
,即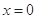 3分
3分
当 时,原不式等价于
时,原不式等价于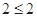 ,即
,即 . 4分
. 4分
当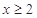 时,原不式等价于
时,原不式等价于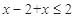 ,即
,即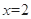 . 5分
. 5分
综上,原不等式的解集为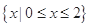 . 6分
. 6分
(2)∵
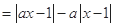 8分
8分
又
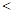 0时,
0时,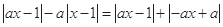
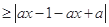


∴
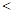 0时,
0时,
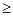
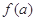 . 12分
. 12分
考点:含绝对值不等式解法,绝对值不等式性质

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 .
. ;
;  ,求证:
,求证:

 ,解不等式
,解不等式 ;
; 有最小值,求
有最小值,求 的取值范围.
的取值范围.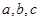 为三角形
为三角形 的三边,求证:
的三边,求证:
 的不等式:
的不等式: 
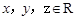 ,且满足:
,且满足: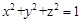 ,
,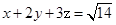 ,求证:
,求证: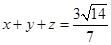 .
. 2
2 .(填不等关系符号)
.(填不等关系符号) +
+ 的最大值是________.
的最大值是________.