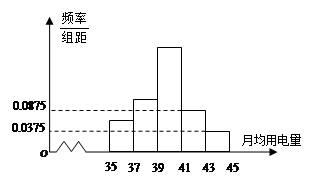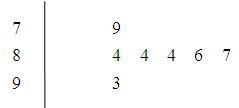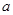题目内容
某电视台举办了“中华好声音”大型歌手选秀活动,过程分为初赛、复赛和决赛,经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图:

赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率;
2、电视台决定,复赛票数不低于85票的选手将成为电视台的“签约歌手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关?
下面临界值表仅供参考:
参考公式:K2=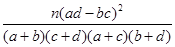 ,其中
,其中

赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率;
2、电视台决定,复赛票数不低于85票的选手将成为电视台的“签约歌手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关?
| | 甲班 | 乙班 | 合计 |
| 签约歌手 | | | |
| 末签约歌手 | | | |
| 合计 | | | |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
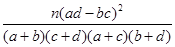 ,其中
,其中
(Ⅰ)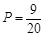 .
.
(Ⅱ)因此在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关.
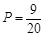 .
. (Ⅱ)因此在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关.
试题分析:(Ⅰ)进入决赛的选手共6名,其中拥有“优先挑战权”的选手共3名. 2分
为拥有“优先挑战权”的选手编号为1,2,3,其余3人编号为A,B,C.
被选中3人的编号所有可能的情况共20种,列举如下:
123,12A,12B,12C,13A,13B,13C,1AB,1AC,1BC,
23A,23B,23C,2AB,2AC,2BC,
3AB,3AC,3BC,
ABC, 4分
其中拥有“优先挑战权”的选手恰有1名的情况共9种,如下:
1AB,1AC,1BC,2AB,2AC,2BC,3AB,3AC,3BC,
∴所求概率为
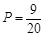 . 6分
. 6分(Ⅱ)
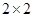 列联表:
列联表:| | 甲班 | 乙班 | 合计 |
| 签约歌手 | 3 | 10 | 13 |
| 未签约歌手 | 17 | 10 | 27 |
| 合计 | 20 | 20 | 40 |
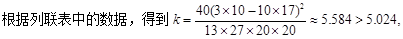
因此在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关. 12分
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。“卡方检验”问题,往往直接套用公式加以计算,对照“定值”比较,作出判断。

练习册系列答案
相关题目
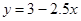 ,则变量
,则变量 增加一个单位时 ( )
增加一个单位时 ( )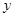 平均增加2.5个单位
平均增加2.5个单位 ,0,1,2,3,,若该样本的平均值为1,则其方差为______________.
,0,1,2,3,,若该样本的平均值为1,则其方差为______________.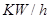 ),将所得数据整理后,画出频率分布直方图如下.直方图中从左到右前3个小矩形的面积之比为
),将所得数据整理后,画出频率分布直方图如下.直方图中从左到右前3个小矩形的面积之比为 ,该乡镇月均用电量在
,该乡镇月均用电量在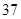 39(
39(