题目内容
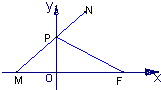 如图所示,设点F坐标为 (1,0 ),点P在y轴上运动,点M在x轴运动上,其中
如图所示,设点F坐标为 (1,0 ),点P在y轴上运动,点M在x轴运动上,其中| PM |
| PF |
| PN |
| MP |
(Ⅰ)求动点N的轨迹E的方程;
(Ⅱ)过点F(1,0 )的直线l和l′分别与曲线E交于A、B两点和C、D两点,若l⊥l′,试求四边形ACBD的面积的最小值.
分析:(Ⅰ)由题意设出M,N,P的坐标,求出所用向量的坐标,联立
•
=0与
=
,消掉M,P的坐标可得N点的轨迹方程;
(Ⅱ)设出直线l的方程,和抛物线方程联立后由弦长公式得到|AB|,设出直线l′的方程,可抛物线联立后由弦长公式求出|CD|,代入四边形面积公式后利用基本不等式求最值.
| PM |
| PF |
| PN |
| MP |
(Ⅱ)设出直线l的方程,和抛物线方程联立后由弦长公式得到|AB|,设出直线l′的方程,可抛物线联立后由弦长公式求出|CD|,代入四边形面积公式后利用基本不等式求最值.
解答:(Ⅰ)设N(x,y ),M (x0,0),P (0,y0),F(1,0 ),
则
=(x0,-y0),
=(x,y-y0),
=(1,-y0),
由
•
=0,得x0+y02=0 ①
由
=
,得
+
=0,得(x+x0,y-2y0)=0,即
,∴
.
代入①得,y2=4x即为所求;
(Ⅱ)设l方程为y=k(x-1),由
,消去x,得y2-
-4=0
设A(x1,y1),B(x2,y2),则y1y2=-4,y1+y2=
,于是
|AB|=
|y1-y2|=
=
=4+
,
设l′的方程为y=-
(x-1),由
,消去x,得y2+4ky-4=0.
设C(x3,y3),D(x4,y4),则y3y4=4,y3+y4=-4k.
∴|CD|=
|y3-y4|=
.
∴|CD|=4+
=4+4k2.
于是SABCD=
|AB|•|CD|=
(4+
)(4+4k2)
=8(2+k2+
)≥8(2+2
)=32.
则
| PM |
| PN |
| PF |
由
| PM |
| PF |
由
| PN |
| MP |
| PN |
| PM |
|
|
代入①得,y2=4x即为所求;
(Ⅱ)设l方程为y=k(x-1),由
|
| 4 |
| k |
设A(x1,y1),B(x2,y2),则y1y2=-4,y1+y2=
| 4 |
| k |
|AB|=
1+
|
(1+
|
(1+
|
| 4 |
| k2 |
设l′的方程为y=-
| 1 |
| k |
|
设C(x3,y3),D(x4,y4),则y3y4=4,y3+y4=-4k.
∴|CD|=
| 1+k2 |
| (1+k2)[(y3+y4)2-4y3y4] |
∴|CD|=4+
| 4 | ||
(-
|
于是SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| k2 |
=8(2+k2+
| 1 |
| k2 |
k2•
|
点评:本题考查了轨迹方程的求法,训练了平面向量的数量积运算,考查了弦长公式的应用及利用基本不等式求最值,关键是能够正确写出对角线互相垂直的四边形的面积,属中高档题.

练习册系列答案
相关题目
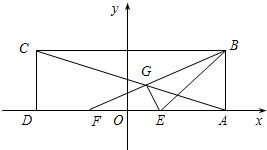 在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.
在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.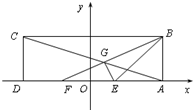 在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.
在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H. 在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点.
在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点.