题目内容
已知椭圆C: 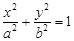 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且经过点P(1,
,且经过点P(1,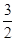 )。
)。
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M。问点M满足什么条件时,圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点,求点D、E距离的最大值。
【答案】
(1)  +
+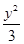 =1
=1
(2) -4<x0<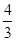
(3) 当x0=-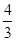 时,DE的最大值为
时,DE的最大值为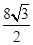
【解析】本试题主要是考查了椭圆方程的求解以及结合圆的知识,求解圆与坐标轴的交点问题,以及直线与圆的位置关系的运用。
解:(1)∵椭圆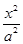 +
+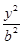 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为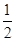 ,且经过点P(1,
,且经过点P(1,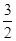 ),
),
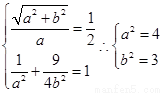
∴椭圆C的方程为 +
+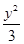 =1。……… 5分
=1。……… 5分
(2)易求得F(1,0)。设M(x0,y0),则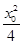 +
+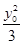 =1,
=1,
圆M的方程为(x-x0)2+(y-y0)2=(1-x0)2+y02,
令x=0,化简得y2-2y0y+2x0-1=0,⊿=4y02-4(2x0-1)2>0……①。
将y02=3(1-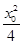 )代入①,得3x02+8x0-16<0,解出 -4<x0<
)代入①,得3x02+8x0-16<0,解出 -4<x0<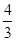 ..........10分
..........10分
(3)设D(0,y1),E(0,y2),其中y1<y2。由(2),得
DE= y2-
y1=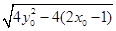 =
= =
=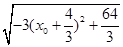 ,
,
当x0=-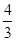 时,DE的最大值为
时,DE的最大值为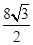

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3. (a>b>0)的离心率为
(a>b>0)的离心率为 短轴一个端点到右焦点的
短轴一个端点到右焦点的 .
. ,求△AOB面积的
,求△AOB面积的 (a>b>0)的离心率为
(a>b>0)的离心率为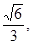 短轴一个端点到右焦点的距离为
短轴一个端点到右焦点的距离为 .
.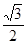 ,求△AOB面积的最大值.
,求△AOB面积的最大值.