题目内容
17.已知△ABC的内角A,B,C所对的边分别为a,b,c且a=3,cosB=$\frac{4}{5}$.(1)若b=6,求sinA的值;
(2)若△ABC的面积S△ABC=$\frac{9}{2}$,求b,c的值.
分析 (1)由条件利用同角三角函数的基本关系求出sinA的值,再利用正弦定理求得 sinA=$\frac{asinB}{b}$ 的值.
(2)由S△ABC=$\frac{9}{2}$,求得c=5,再利用余弦定理求得b的值.
解答 解:(1)∵cosB=$\frac{4}{5}$,∴sinB=1-cos2B=$\frac{3}{5}$.
由正弦定理得$\frac{a}{sinA}$=$\frac{b}{sinB}$,∴sinA=$\frac{asinB}{b}$=$\frac{3×\frac{3}{5}}{6}$=$\frac{3}{10}$.
(2)∵△ABC的面积S△ABC =$\frac{1}{2}$ac•sinB=$\frac{1}{2}×3×c×\frac{3}{5}$=$\frac{9}{2}$,∴c=5.
由余弦定理得b=$\sqrt{{c}^{2}{+a}^{2}-2ac•cosB}$=$\sqrt{25+9-2×a×5×\frac{4}{5}}$=$\sqrt{10}$.
点评 本题主要考查同角三角函数的基本关系,正弦定理和余弦定理的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
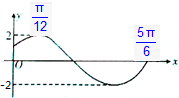 如图是f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象,求函数f(x)的解析式.
如图是f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象,求函数f(x)的解析式.