题目内容
已知函数f(x)=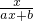 (a、b是非零实常数)满足f(1)=
(a、b是非零实常数)满足f(1)= ,且方程f(x)=x有且仅有一个实数解.
,且方程f(x)=x有且仅有一个实数解.
(1)求a、b的值;
(2)在直角坐标系中,求定点A(0,2)到函数f(x)图象上任意一点P(x,y)的距离|AP|的最小值.
(3)当x∈(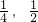 ]时,不等式(x+1)•f(x)>m(m-x)-1恒成立,求实数m的取值范围.
]时,不等式(x+1)•f(x)>m(m-x)-1恒成立,求实数m的取值范围.
解:(1)∵f(x)=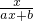 ,且f(1)=
,且f(1)= ,
,
∴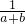 =
= ,即a+b=2;
,即a+b=2;
又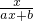 =x有且仅有一个实数解,
=x有且仅有一个实数解,
∴x(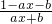 )=0有且仅有一个实数解,为0.
)=0有且仅有一个实数解,为0.
∴b=1,a=1.
∴f(x)= .
.
(2)由(1)知,P(x, ),
),
|AP|2= +x2
+x2
=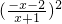 +x2
+x2
=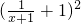 +[(x+1)-1]2,
+[(x+1)-1]2,
令t= ,
,
则|AP|2=t2+2t+1+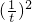 -
- +1
+1
=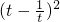 +2(t-
+2(t- )+4,
)+4,
令r=t- ,
,
则|AP|2=r2+2r+4=(r+1)2+3,
∴当r=-1,即t- =-1,t=
=-1,t=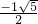 时,|AP|的最小值为
时,|AP|的最小值为 .
.
(3)∵x∈(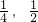 ],
],
∴x+1> >0,
>0,
∴(x+1)•f(x)>m(m-x)-1恒成立?x>m(m-x)-1恒成立?(1+m)x>m2-1,
当m+1>0,即m>-1时,
有m-1<x恒成立?m<x+1?m<(x+1)min,
∴-1<m< ;
;
当m+1<0,即m<-1时,同理可得m>(x+1)max= ,
,
∴此时m不存在.
综上得-1<m< .
.
分析:(1)依题意,a+b=2,由x(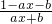 )=0有且仅有一个实数解x=0可求得b=1,a=1;
)=0有且仅有一个实数解x=0可求得b=1,a=1;
(2)由(1)知,P(x, ),从而可得|AP|2=
),从而可得|AP|2=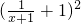 +[(x+1)-1]2,通过换元,令t=
+[(x+1)-1]2,通过换元,令t= ,得|AP|2=
,得|AP|2=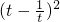 +2(t-
+2(t- )+4,再令r=t-
)+4,再令r=t- ,通过配方即可求得|AP|的最小值;
,通过配方即可求得|AP|的最小值;
(3)依题意,x∈(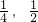 ]时,不等式(x+1)•f(x)>m(m-x)-1恒成立?(1+m)x>m2-1恒成立,通过对m+1>0与m+1<0的讨论,结合函数恒成立问题即可求得实数m的取值范围.
]时,不等式(x+1)•f(x)>m(m-x)-1恒成立?(1+m)x>m2-1恒成立,通过对m+1>0与m+1<0的讨论,结合函数恒成立问题即可求得实数m的取值范围.
点评:本题考查函数恒成立问题,考查方程思想、分类讨论思想与等价转化思想的综合应用,考查换元法与配方法,考查推理与运算能力,属于难题.
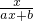 ,且f(1)=
,且f(1)= ,
,∴
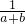 =
= ,即a+b=2;
,即a+b=2;又
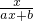 =x有且仅有一个实数解,
=x有且仅有一个实数解,∴x(
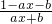 )=0有且仅有一个实数解,为0.
)=0有且仅有一个实数解,为0.∴b=1,a=1.
∴f(x)=
 .
.(2)由(1)知,P(x,
 ),
),|AP|2=
 +x2
+x2=
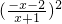 +x2
+x2=
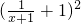 +[(x+1)-1]2,
+[(x+1)-1]2,令t=
 ,
,则|AP|2=t2+2t+1+
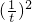 -
- +1
+1=
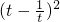 +2(t-
+2(t- )+4,
)+4,令r=t-
 ,
,则|AP|2=r2+2r+4=(r+1)2+3,
∴当r=-1,即t-
 =-1,t=
=-1,t=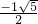 时,|AP|的最小值为
时,|AP|的最小值为 .
.(3)∵x∈(
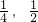 ],
],∴x+1>
 >0,
>0,∴(x+1)•f(x)>m(m-x)-1恒成立?x>m(m-x)-1恒成立?(1+m)x>m2-1,
当m+1>0,即m>-1时,
有m-1<x恒成立?m<x+1?m<(x+1)min,
∴-1<m<
 ;
;当m+1<0,即m<-1时,同理可得m>(x+1)max=
 ,
,∴此时m不存在.
综上得-1<m<
 .
.分析:(1)依题意,a+b=2,由x(
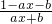 )=0有且仅有一个实数解x=0可求得b=1,a=1;
)=0有且仅有一个实数解x=0可求得b=1,a=1;(2)由(1)知,P(x,
 ),从而可得|AP|2=
),从而可得|AP|2=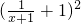 +[(x+1)-1]2,通过换元,令t=
+[(x+1)-1]2,通过换元,令t= ,得|AP|2=
,得|AP|2=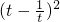 +2(t-
+2(t- )+4,再令r=t-
)+4,再令r=t- ,通过配方即可求得|AP|的最小值;
,通过配方即可求得|AP|的最小值;(3)依题意,x∈(
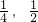 ]时,不等式(x+1)•f(x)>m(m-x)-1恒成立?(1+m)x>m2-1恒成立,通过对m+1>0与m+1<0的讨论,结合函数恒成立问题即可求得实数m的取值范围.
]时,不等式(x+1)•f(x)>m(m-x)-1恒成立?(1+m)x>m2-1恒成立,通过对m+1>0与m+1<0的讨论,结合函数恒成立问题即可求得实数m的取值范围.点评:本题考查函数恒成立问题,考查方程思想、分类讨论思想与等价转化思想的综合应用,考查换元法与配方法,考查推理与运算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|