题目内容
已知条件p:x2-4≤0,条件q:
≥0,则¬p是q的( )
| x+2 |
| x-2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出满足条件¬p的x的范围,和满足条件q的x的范围,判断两个范围的包含关系,进而可用集合法判断出¬p与q的充要关系.
解答:解:∵条件p:x2-4≤0,
∴条件¬p:x2-4>0,即x∈(-∞,-2)∪(2,+∞);
∵条件q:
≥0,即x∈(-∞,-2]∪(2,+∞);
且(-∞,-2)∪(2,+∞)?(-∞,-2]∪(2,+∞);
故¬p是q的充分不必要条件,
故选:A
∴条件¬p:x2-4>0,即x∈(-∞,-2)∪(2,+∞);
∵条件q:
| x+2 |
| x-2 |
且(-∞,-2)∪(2,+∞)?(-∞,-2]∪(2,+∞);
故¬p是q的充分不必要条件,
故选:A
点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,已知1≤S2≤2,3≤S4≤5,则S6的取值范围是( )
| A、[3,12] | B、[4,12] | C、[5,11] | D、[5,8] |
下列有关命题的说法正确的是( )
| A、命题“x2=1,则x=1”的否命题为“若x2=1,则x≠1” | B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” | C、若“p∨q”为真命题,则p,q至少有一个为真命题 | D、命题“若x=y,则sinx=siny”的逆命题为假命题 |
不等式x+
≥2成立的一个必要不充分条件是( )
| 1 |
| x |
| A、(0,+∞) |
| B、(0,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
sinα=sinβ是α=β的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分又不必要条件 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=3x2+5,则从0.1到0.2的平均变化率为( )
| A、0.3 | B、0.6 | C、0.9 | D、1.2 |
若复数z1=1+2i,z2=1-i,其中i是虚数单位,则(z1+z2)i在复平面内对应的点在( )
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
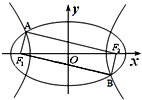 如图,F1、F2是椭圆C1与双曲线C2:
如图,F1、F2是椭圆C1与双曲线C2: