题目内容
如图,在三棱锥P -ABC中,点P在平面ABC上的射影D是AC的中点.BC ="2AC=8,AB" =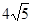
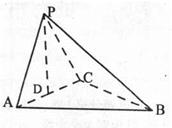
(I )证明:平面PBC丄平面PAC
(II)若PD =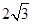 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值.
(I) 通过证明AC⊥BC,进而证明BC⊥平面PAC,从而得证;
(II) 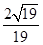
【解析】
试题分析:
(Ⅰ)证明: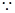 点
点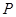 在平面
在平面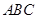 上的射影
上的射影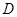 是
是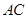 的中点,
的中点,
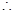 PD⊥平面ABC,PD
PD⊥平面ABC,PD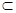 平面PAC
平面PAC
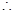 平面PAC⊥平面ABC
……2分
平面PAC⊥平面ABC
……2分
 BC=2AC=8,AB=4
BC=2AC=8,AB=4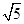
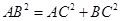 ,故AC⊥BC
……4分
,故AC⊥BC
……4分
又平面PAC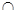 平面ABC=AC,BC
平面ABC=AC,BC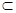 平面ABC
平面ABC
BC⊥平面PAC,又BC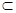 平面PBC
平面PBC
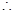 平面PBC⊥平面PAC ……6分
平面PBC⊥平面PAC ……6分
(Ⅱ)如图所示建立空间直角坐标系,

则C(0,0,0),A(4,0,0),B(0,8,0),P(2,0,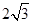 ),
),
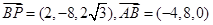 ……8分
……8分
设平面PAB的法向量为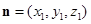
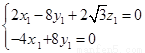
令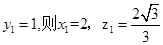
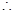
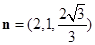
设平面PBC的法向量为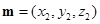
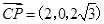 ,
,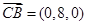
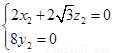
令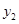 =0,
=0, =1,
=1,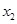 =-
=-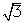 ,
,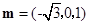 ……10分
……10分
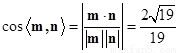
 二面角
二面角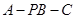 的平面角的余弦值为
的平面角的余弦值为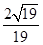 ……12分
……12分
考点:本小题主要考查面面垂直的证明和二面角的求法.
点评:立体几何问题,主要是考查学生的空间想象能力和逻辑推理能力,解决此类问题时,要紧扣相应的判定定理和性质定理,要将定理中要求的条件一一列举出来,缺一不可,用空间向量解决立体几何问题时,要仔细运算,适当转化.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案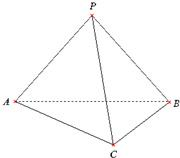 如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.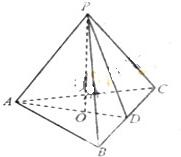 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上. 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,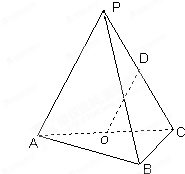 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC,点O、D分别是AC、PC的中点.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC,点O、D分别是AC、PC的中点. 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为