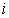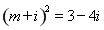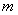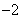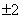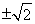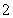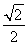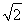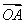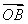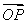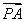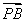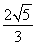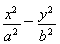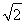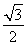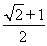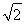题目内容
已知圆C经过点A(－2,0)，B(0,2)，且圆心C在直线y＝x上，又直线l：y＝kx＋1与圆C相交于P、Q两点．
(1)求圆C的方程；
(2)若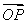
·
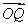＝－2，求实数k的值．
（1）x2＋y2＝4（2）k＝0.
【解析】(1)设圆心C(a，a)，半径为r.
因为圆C经过点A(－2,0)，B(0,2)，
所以|AC|＝|BC|＝r，易得a＝0，r＝2，
所以圆C的方程是x2＋y2＝4.
(2)因为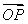
·
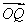＝2×2×cos〈
，
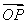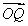〉＝－2，且
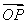与
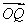的夹角为∠POQ，
所以cos∠POQ＝－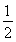
，∠POQ＝120°，
所以圆心C到直线l：kx－y＋1＝0的距离d＝1，
又d＝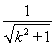
，所以k＝0.
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程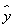
＝3－5x，变量x增加一个单位时，y平均增加5个单位；
③线性回归方程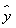
＝
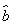x＋
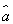必过(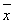
，
)；
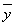④在一个2×2列联表中，由计算得K2＝13.079，则有99%的把握确认这两个变量间有关系．
其中错误的个数是( )
本题可以参考独立性检验临界值表：
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A．0 B．1 C．2 D．3
