题目内容
8.求函数y=$\sqrt{sinx+cosx}$+lgsin2x+$\sqrt{9-{x}^{2}}$的定义域.分析 根据三角形函数对数函数的性质即可求出函数的定义域.
解答 解:∵函数y=$\sqrt{sinx+cosx}$+lgsin2x+$\sqrt{9-{x}^{2}}$的定义域,
∴$\left\{\begin{array}{l}{sinx+cosx≥0}\\{sin2x>0}\\{9-{x}^{2}≥0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2kπ≤x+\frac{π}{4}≤2kπ+π}\\{2kπ<2x<2kπ+π}\\{-3≤x≤3}\end{array}\right.$,k∈z,
当k=0时,0<x<$\frac{π}{2}$,当k=-1时,-3≤x<-$\frac{π}{2}$,当k=1时,为空集,
综上所述函数的定义域为[-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$)
点评 本题考查了函数的定义域的求法,关键是掌握三角形函数对数函数即二次根式的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
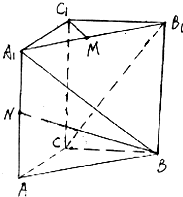 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.