题目内容
19.已知数列{an}的前n项和为Sn,且Sn+pan=p(p$>\frac{3}{4}$).(1)求a1;
(2)求数列{an}的通项公式;
(3)对于n∈N+,若不等式$\frac{1}{(4p-2)-4(p+1){a}_{n}}$>1当且仅当n=2时成立,求p的取值范围.
分析 (1)直接在数列递推式中取n=1求得首项;
(2)在数列递推式中取n=n-1得另一递推式,和原递推式作差后可得数列{an}为等比数列,由等比数列的通项公式得答案;
(3)把$\frac{1}{(4p-2)-4(p+1){a}_{n}}$>1当且仅当n=2时成立,转化为$\frac{(p+1)^{n-1}}{(4p-2)(p+1)^{n-1}-4{p}^{n}}$>1当且仅当n=2时成立,然后求出n=1,n=3时不等式不成立的p的范围,求出n=2时不等式成立的p的范围,进一步说明当n≥3时,数列{$\frac{4{p}^{n}}{(p+1)^{n-1}}$}递减,且(4p-2)-$\frac{4{p}^{n}}{(p+1)^{n}}$>0即可得到当且仅当n=2时不等式成立的p的取值范围是(1,3).
解答 解:(1)由Sn+pan=p,得a1+pa1=p,
∴(1+p)a1=p,
即${a}_{1}=\frac{p}{1+p}$;
(2)由Sn+pan=p,得
当n≥2时,Sn-1+pan-1=p,
两式作差得:an+pan-pan-1=0,即(1+p)an=pan-1,
∵${a}_{1}=\frac{p}{1+p}≠0$,
∴数列{an}是以$\frac{p}{1+p}$为首项,以$\frac{p}{1+p}$为公比的等比数列,
则${a}_{n}=\frac{p}{1+p}•(\frac{p}{1+p})^{n-1}=(\frac{p}{1+p})^{n}$;
(3)由$\frac{1}{(4p-2)-4(p+1){a}_{n}}$>1当且仅当n=2时成立,
得$\frac{1}{(4p-2)-4(p+1)•\frac{{p}^{n}}{(p+1)^{n}}}$=$\frac{1}{\frac{(4p-2)•(p+1)^{n-1}-4{p}^{n}}{(p+1)^{n-1}}}$
=$\frac{(p+1)^{n-1}}{(4p-2)•(p+1)^{n-1}-4{p}^{n}}$>1当且仅当n=2时成立,
当n=1时,$\frac{(p+1)^{0}}{(4p-2)•(p+1)^{0}-4p}=-\frac{1}{2}≤1$对于p$>\frac{3}{4}$成立;
当n=2时,要使$\frac{p+1}{(4p-2)(p+1)-4{p}^{2}}>1$成立,即$\frac{p-3}{p-1}<0$,∴1<p<3;
当n=3时,要使$\frac{(p+1)^{2}}{(4p-2)(p+1)^{2}-4{p}^{3}}≤1$成立,即$\frac{5{p}^{2}-2p-3}{3{p}^{2}-1}≥0$成立,
也就是p>1成立;
由当p>1,且n≥3时,数列{$\frac{4{p}^{n}}{(p+1)^{n-1}}$}递减,且(4p-2)-$\frac{4{p}^{n}}{(p+1)^{n}}$>0,
∴当p>1,且n≥3时,不等式$\frac{1}{(4p-2)-4(p+1){a}_{n}}$≤1恒成立.
故使不等式$\frac{1}{(4p-2)-4(p+1){a}_{n}}$>1当且仅当n=2时成立的p的取值范围是(1,3).
点评 本题考查了等比关系的确定,考查了等比数列的通项公式的求法,考查了数列的函数特性,体现了分类讨论的数学思想方法,属难题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=4x |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 在角
在角 的终边上,则
的终边上,则 的值为( )
的值为( )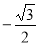 B.
B.
 D.
D.