题目内容
【题目】已知数列
是公比大于
的等比数列，
为数列的前
项和，
，且
，
，
成等差数列.数列
的前项和为
，
满足
，且
，
（1）求数列和的通项公式；
（2）令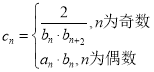
，求数列
的前
项和为
；
（3）将数列，的项按照“当为奇数时，
放在前面；当为偶数时，
放在前面”的要求进行排列，得到一个新的数列：
，
，
，
，
，
，
，
，
，
，
，
，求这个新数列的前项和
.
【答案】（1）
,
（2）
（3）
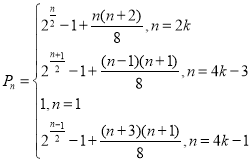
【解析】
（1）设等比数列
的公比为
，依题意得到关于
、的方程组解得，由
，可知
是首项为
，公差为
的等差数列，求出的通项公式，即可求出
的通项公式；
（2）利用分组求和，错位相减，裂项相消求其前
项和为
；
（3）分
，
，
，三种情况讨论可得；
解：（1）设等比数列的公比为，
由已知，得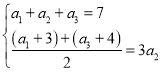
，
即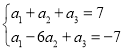
，也即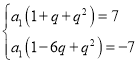
解得
故数列的通项为.
，
是首项为，公差为的等差数列，
，
（2）
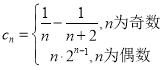
其中
令
则
①
②
①减②得
，
∴
（3）数列前
项和
，数列的前项和
；
①当，
②当
⑴当
时，
⑵当
时，
③当
综上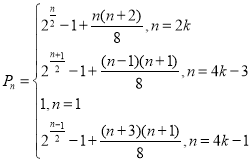
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
