题目内容
有以下四个命题:
①4名同学分别报名参加学校组织的数学、物理、化学三个项目的竞赛,每人限报其中的一项,不同报法的种数是43;
②4名同学分3张有座足球票,每人至多分l张,而且必须分完,那么不同分法的种数是C43;
③从含有98件正品,2件次品的100件产品中任意抽取3件,抽取的这3件产品中至少有l件次品的概率是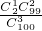 ;
;
④在(1-x)2n+1(n∈N*)的二项展开式中,系数最大的项是第n+1项,系数最小的项是第n+2项.
其中真命题是________.
①
分析:根据排列组合即简单计数问题看出前两个命题的真假,根据等可能事件的概率做出第三个命题的真假,根据二项式定理的性质得到第四个命题的真假,得到结论.
解答:4名同学分别报名参加学校组织的数学、物理、化学三个项目的竞赛,
每人限报其中的一项,不同报法的种数是34,故①不正确.
4名同学分3张有座足球票,每人至多分l张,而且必须分完,那么不同分法是从四个人中选三个人种数是C43;故②正确.
从含有98件正品,2件次品的100件产品中任意抽取3件,
抽取的这3件产品中至少有l件次品的概率是 ,故③不正确,
,故③不正确,
根据二项式系数的性质知,在(1-x)2n+1(n∈N*)的二项展开式中,展开式共有2n+2项
系数最大的项是第n+2项,系数最小的项是第n+1项.故④不正确,
综上可知只有①正确,
故答案为:①
点评:本题考查排列组合即简单计数问题,考查等可能事件的概率,考查二项式性质的应用,本题解题的关键是需要做出四个问题的正确结果,本题是一个中档题目.
分析:根据排列组合即简单计数问题看出前两个命题的真假,根据等可能事件的概率做出第三个命题的真假,根据二项式定理的性质得到第四个命题的真假,得到结论.
解答:4名同学分别报名参加学校组织的数学、物理、化学三个项目的竞赛,
每人限报其中的一项,不同报法的种数是34,故①不正确.
4名同学分3张有座足球票,每人至多分l张,而且必须分完,那么不同分法是从四个人中选三个人种数是C43;故②正确.
从含有98件正品,2件次品的100件产品中任意抽取3件,
抽取的这3件产品中至少有l件次品的概率是
 ,故③不正确,
,故③不正确,根据二项式系数的性质知,在(1-x)2n+1(n∈N*)的二项展开式中,展开式共有2n+2项
系数最大的项是第n+2项,系数最小的项是第n+1项.故④不正确,
综上可知只有①正确,
故答案为:①
点评:本题考查排列组合即简单计数问题,考查等可能事件的概率,考查二项式性质的应用,本题解题的关键是需要做出四个问题的正确结果,本题是一个中档题目.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 ;
;