题目内容
对于函数f（x）=1-2cos2（x+
），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
）上单调递减，④x=
是f（x）的一条对称轴．其中真命题有（ ）
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| A、1个 | B、2个 |
| C、.3个 | D、.4个 |
分析：利用二倍角余弦公式对解析式进行化简后，再判断出函数的奇偶性、求出函数的最小正周期，判断①②，根据正弦函数的单调性和对称性进行判断③④．
解答：解：f（x）=1-2cos2（x+
）=-cos（2x+
）=sin2x，
则此函数为奇函数，且周期T=π，故①②正确；因函数在（0，
）单调递增，故③不对；
由2x=
+kπ解得，函数的对称轴x=
+
（k∈Z），故④不对．
故选B．
| π |
| 4 |
| π |
| 2 |
则此函数为奇函数，且周期T=π，故①②正确；因函数在（0，
| π |
| 4 |
由2x=
| π |
| 2 |
| π |
| 4 |
| kπ |
| 2 |
故选B．
点评：本题主要考查了正弦函数的性质的应用，需要利用倍角公式对解析式进行化简后，再由正弦函数的性质进行判断，考查了整体思想的应用．
练习册系列答案
相关题目
），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
是f（x）的一条对称轴．其中真命题有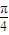
），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
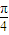）上单调递减，④x=
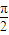是f（x）的一条对称轴．其中真命题有（ ）
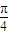），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
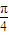）上单调递减，④x=
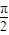是f（x）的一条对称轴．其中真命题有（ ）