题目内容
定义在R上的函数f(x)满足f(-x)=-f(x),f(x)=-f(x+2),且x∈(-1,0)时,f(x)=2x+
,则f(log220)=______.
| 1 |
| 5 |
∵f(-x)=-f(x),
∴f(x)为奇函数,
∵f(x)=-f(x+2),即f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是周期函数,周期为4,
∵log216<log220<log232,
∴4<log220<5,
∴0<log220-4<1,即0<log2
<1,即-1<log2
<0,
∴f(log220)=f(log220-4)=f(log2
)=-f(-log2
)=-f(log2
),
∵x∈(-1,0)时,f(x)=2x+
,
∴f(log2
)=2log2
+
=
+
=1,
∴f(log220)=-1.
故答案为:-1.
∴f(x)为奇函数,
∵f(x)=-f(x+2),即f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是周期函数,周期为4,
∵log216<log220<log232,
∴4<log220<5,
∴0<log220-4<1,即0<log2
| 5 |
| 4 |
| 4 |
| 5 |
∴f(log220)=f(log220-4)=f(log2
| 5 |
| 4 |
| 5 |
| 4 |
| 4 |
| 5 |
∵x∈(-1,0)时,f(x)=2x+
| 1 |
| 5 |
∴f(log2
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∴f(log220)=-1.
故答案为:-1.

练习册系列答案
相关题目
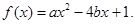
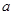 和
和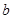 ,
,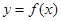 在区间[
在区间[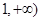 上是增函数的概率;
上是增函数的概率;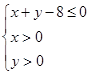 内的随机点,求函数
内的随机点,求函数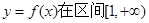 上是增函数的概率.
上是增函数的概率.
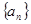 的前n项和为
的前n项和为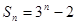 ,则
,则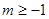 ,则函数
,则函数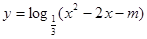 的值域为R;
的值域为R;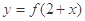 与函数
与函数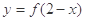 的图象关于直线x=2对称;
的图象关于直线x=2对称;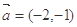 与
与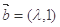 的夹角为钝角,则实数
的夹角为钝角,则实数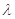 的取值范围是
的取值范围是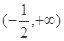 ;
;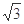 的圆锥,过顶点的一个截面面积的最大值为
的圆锥,过顶点的一个截面面积的最大值为 ,则
,则 。
。