题目内容
某船开始看见灯塔在南偏东30°方向，后来船沿南偏东60°的方向航行45km后，看见灯塔在正西方向，则这时船与灯塔的距离是（ ）
A．15
| B．30km | C．15km | D．15
|
设灯塔位于A处，船开始的位置为B，航行45km后处C处，如图所示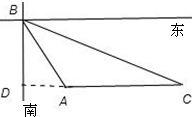
∠DBC=60°，∠ABD=30°，BC=45
∴∠ABC=60°-30°=30°，∠BAC=180°-60°=120°．
△ABC中，由正弦定理
=
，
可得AC=
=
×
=15
（km）．
即船与灯塔的距离是15
（km）．
故选：A
∠DBC=60°，∠ABD=30°，BC=45
∴∠ABC=60°-30°=30°，∠BAC=180°-60°=120°．
△ABC中，由正弦定理
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
可得AC=
| BCsin∠ABC |
| sin∠BAC |
| 45 | ||||
|
| 1 |
| 2 |
| 3 |
即船与灯塔的距离是15
| 3 |
故选：A
练习册系列答案
相关题目
则cos A= .
，则△ABC一定是( )